این قسمت دوم از آموزشهای ریاضی مربوط به ماشینهای بردار پشتیبان است. اگر قسمتهای قبلی را هنوز مطالعه نکردهاید، میتوانید آموزش را از قسمت اول با مطالعه مقاله: SVM – درک مفاهیم ریاضی مورد نیاز – قسمت اولشروع کنید.
در قسمت اول مزیت استفاده از SVM را باهم بررسی کردیم. هدف آن پیدا کردن ابرصفحه جداکنندهای بود که حاشیه را به حداکثر برساند.
ولی چطور این حاشیه را محاسبه میکنیم؟
SVM = Support VECTOR Machine
در عبارت ماشین بردار پشتیبان کلمه بردار وجود دارد.
این یعنی درک بردار و چگونگی استفاده از آن برای ما اهمیت دارد.
اجازه دهید جمعبندی کوتاهی از مواردی که امروز بررسی خواهیم کرد، داشته باشیم:
- بردار چیست؟
- اندازه بردار
- جهت بردار
- جمع و تفاضل بردارها
- جمع نقطهای چیست؟
- تصویر یک بردار روی برداری دیگر
پس از آشنا شدن با موارد بالا، در ادامه خواهیم دید:
- معادله ابرصفحه چیست؟
- حاشیه را چطور محاسبه کنیم؟
بردار چیست؟
اگر نقطهای مانند ![]() را تعریف کنیم، در صفحه
را تعریف کنیم، در صفحه ![]() میتوانیم آن را به صورت زیر رسم کنیم:
میتوانیم آن را به صورت زیر رسم کنیم:
شکل ۱: یک نقطه
تعریف: هر نقطه ![]() در
در ![]() ، یک بردار در صفحه را مشخص میکند که ابتدای آن مبدا مختصات و انتهای آن همان نقطه
، یک بردار در صفحه را مشخص میکند که ابتدای آن مبدا مختصات و انتهای آن همان نقطه ![]() است.
است.
این تعریف به این معنی است که بین مبدا مختصات و نقطه ![]() ، یک بردار وجود دارد.
، یک بردار وجود دارد.
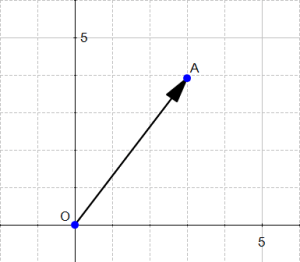
شکل ۲: یک بردار
اگر به این صورت بگیم که شروه در نقطه![]() است، در این صورت بردار بالا، همان بردار
است، در این صورت بردار بالا، همان بردار ![]() است. همچنین میتوانیم اسم دلخواهی مانند
است. همچنین میتوانیم اسم دلخواهی مانند ![]() را برای آن در نظر بگیریم.
را برای آن در نظر بگیریم.
توجه: نام بردار را میتوان هم با فلشی بالای ان و هم به صورت ضخیم نمایش داد.در اینجا من از فلش بالای نام بردار مانند:![]() که از دو حرف انگلیسی تشکیل شده، استفاده میکنم. و زمانی که اسم بردار تک حرفی باشد، آن را به صورت ضخیم(Bold) مینویسم.
که از دو حرف انگلیسی تشکیل شده، استفاده میکنم. و زمانی که اسم بردار تک حرفی باشد، آن را به صورت ضخیم(Bold) مینویسم.
تا اینجا فهمیدیم که با چیزی به اسم بردار سروکار داریم. ولی به احتمال زیاد هنوز نمیدانیم که بردار چیست؟
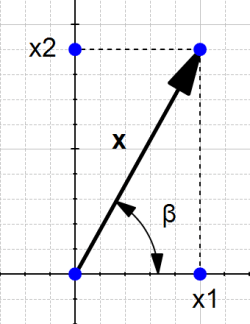
تعریف: بردار شیٔای است دارای جهت و اندازه.
که در ادامه به این دو مفهوم میپردازیم.
۱) اندازه
اندازه یا طول بردار ![]() به صورت
به صورت ![]() نوشته و به آن نرم گفته میشود.
نوشته و به آن نرم گفته میشود.
برای بردار ![]() ،
، ![]() طول ضلع
طول ضلع ![]() است.
است.
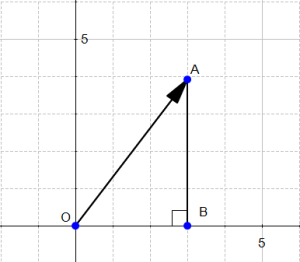
شکل ۳
در شکل ۳ به راحتی میتوانیم فاصله OA را به کمک قضیه فیثاغورث محاسبه کنیم:
![]()
![]()
![]()
![]()
![]()
۲) جهت
جهت دومین جزٔ یک بردار است.
تعریف: جهت یک بردار مانند ![]() ، بردار
، بردار ![]() است.
است.
مختصات w از کجا میاد؟
درک کردن تعریف
برای پیدا کردن جهت یک بردار، به زاویههای آن نیاز خواهیم داشت
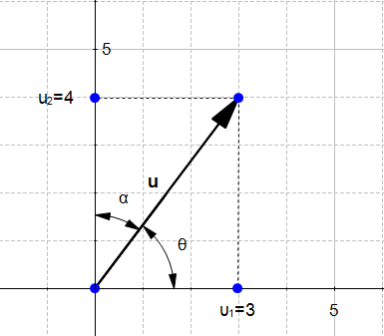
شکل ۴: جهت یک بردار
شکل ۴ بردار ![]() را با مختصات
را با مختصات ![]() و
و ![]() نشان میدهد.
نشان میدهد.
تعریف قبل را به این صورت نیز میتوان بیان کرد:
تعریف سادهتر ۱: جهت بردار u به وسیله زاویه بردار با محور افقی که آن را ![]() و زاویه بردار با محور عمودی که آن را
و زاویه بردار با محور عمودی که آن را ![]() مینامیم، تعریف میشود.
مینامیم، تعریف میشود.
برای سادهتر شدن از کسینوس زاویهها استفاده میکنیم.
در یک مثلث قائمالزاویه، کسینوس زاویه ![]() به صورت زیر محاسبه میشود.
به صورت زیر محاسبه میشود.
![]()
در شکل ۴ میتوان مشاهده کرد که، دو مثل قائمالزاویه میتواند وجود داشته باشد و در هر دو حالت، ضلع مجاور یکی از محورها خواهد بود. این یعنی تعریف کسینوس بهطور ضمنی محور مرتبط با زاویه را در بر میگیرد. در نتیجه تعریف ساده قبلی را به صورت زیر نیز میتوان نوشت:
تعریف ساده ۲: جهت بردار u به وسیله کسینوس زاویه ![]() و کسینوس زاویه
و کسینوس زاویه ![]() تعریف میشود.
تعریف میشود.
![]()
![]()
با توجه به مقدار اولیه بردار W، دلیل نامگذاری مختصات آن به جهت کسینوسی اکنون برای ما مشخص شده است.
![]()
و
![]()
جهت بردار ![]() ، بردار
، بردار ![]() است.
است.
اگر این بردار را رسم کنیم، شکل ۵ را خواهیم داشت:
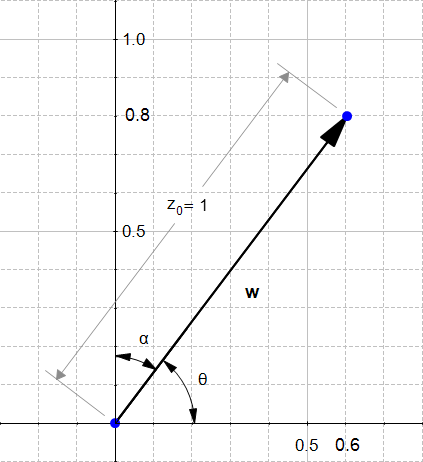
شکل ۵: جهت بردار u
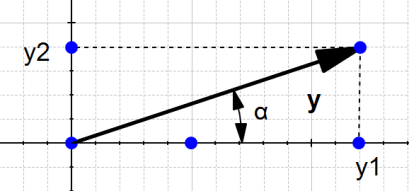
میتوان مشاهده کرد که w در واقع از نظر ظاهری بسیار شبیه u است، به جز اینکه w کمی کوچکتر است. نکته جالبی که در مورد بردارهای جهت وجود دارد این است که نرم آنها همیشه برابر با ۱ است. به همین دلیل آنها را بردارهای واحد مینامیم.
جمع دو بردار
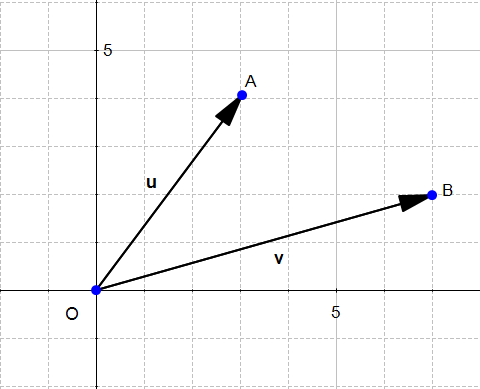
شکل ۶: دو بردار u و v
اگر دو بردار ![]() و
و ![]() را داشته باشیم، در این صورت جمع آنها به صورت زیر خواهد بود:
را داشته باشیم، در این صورت جمع آنها به صورت زیر خواهد بود:
![]()
به این معنی که جمع دو بردار، به ما بردار سومی را خواهد داد که مختصات آن برابر است با جمع مختصات بردارهای اولیه.
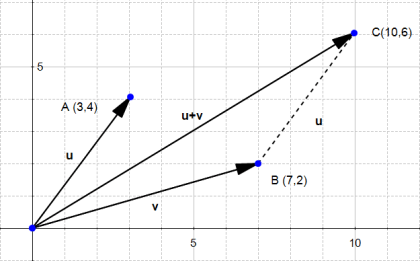
شکل ۷: جمع دو بردار
تفاضل بین دو بردار
تفاضل دو بردار هم مشابه جمع آنها عمل میکند.
![]()
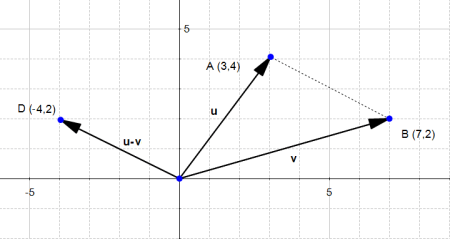
شکل ۸: تفاضل دو بردار
از آنجایی که عمل تفاضل دارای خاصیت جابجایی است، میتوان حالت دیگری را نیز در نظر گرفت:
![]()
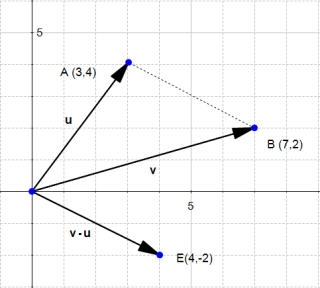
شکل ۹: تفاضل u – v
دو تصویر آخر، بردارهای درستی که توسط تفاضل بردارهای u و v به دست آمدهاند را نمایش میدهند.
با این حال، از آنجایی که یک بردار اندازه و جهت دارد، معمولا ما بردار موازی با بردار تفاضل(برداری با اندازه و جهت یکسان که نقطه شروع آن مبدا مختصات نیست) را در نظر میگیریم که با بردار اصلی برابر است و فقط در مکان دیگری از صفحه رسم شده است.
پس اگر جایی بردار تفاضلی به صورت زیر دیدید تعجب نکنید:
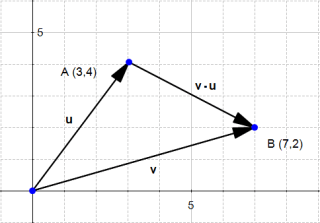
شکل ۱۰: راه دیگری برای نمایش تفاضل v – u
و
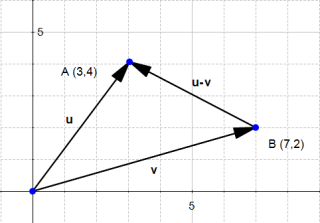
شکل ۱۱: راه دیگری برای نمایش تفاضل u – v
با توجه به ریاضیات ممکن است که این نوع نمایش اشتباه به نظر برسد. به دلیل این که انتهای بردار u – v در نقطه صحیحی قرار نمیگیرد. ولی این یک راه آسان برای فکر کردن در مورد بردارها است که معمولا ما ترجیح میدهیم به این صورت با آنها برخورد کنیم.
ضرب نقطهای
یکی ار علائمی که برای فهم SVM خیلی مهم است، ضرب نقطهای نام دارد.
تعریف: از لحاظ هندسی، ضرب اندازههای اقلیدسی دو بردار و کسینوس زاویه بین آنها، ضرب برداری نام دارد.
که یعنی اگر ما دو بردار x و y را داشته باشیم و زاویه بین آنها برابر ![]() باشد، ضرب نقطهای آنها برابر است با:
باشد، ضرب نقطهای آنها برابر است با:
![]()
چرا؟
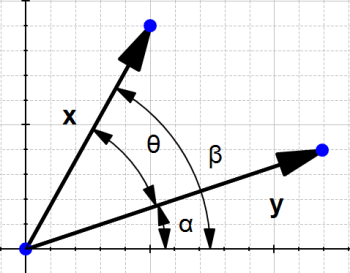
برای پاسخ دادن به این سؤال، به مسأله از لحاظ هندسی نگاه میکنیم.
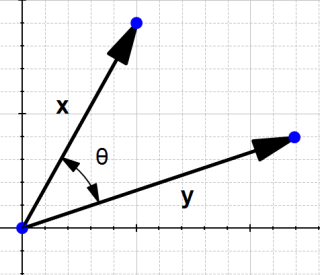
شکل ۱۲
در تعریف، از ![]() صحبت شد، پس بررسی میکنیم که این
صحبت شد، پس بررسی میکنیم که این ![]() چیست؟
چیست؟
طبق تعریف میدانیم که در یک مثلث قائمالزاویه:
![]()
ولی در شکل مثلث قائمالزاویهای وجود ندارد.
با این حال اگر از زاویه دیگری به شکل ۱۲ نگاه کنیم، میتوانیم دو مثلث قائمالزاویه که هر بردار با محور افقی ایجاد میکند را پیدا کنیم.
شکل ۱۳
و
شکل ۱۴
پس شکل مسأله زیر را میتوان به صورت زیر نشان داد:
شکل ۱۵
میتوان مشاهده کرد که
![]()
پس محاسبه ![]() به محاسبه
به محاسبه ![]() تبدیل شد.
تبدیل شد.
فرمول خاصی به نام کسینوس تفاضل دو زاویه وجود دارد که به صورت زیر نوشته میشود:
![]()
(در صورت تمایل میتوانید توضیحات بیشتر راجع به این فرمول را در اینجا بخوانید.)
اجازه دهید از این فرمول استفاده کنیم!
![]()
![]()
![]()
![]()
پس اگر هر عبارت را جایگزین کنیم داریم
![]()
![]()
اگر دو طرف را در ![]() ضرب کیم داریم:
ضرب کیم داریم:
![]()
که برابر است با:
![]()
فرمولی که همین الآن به آن رسیدیم، تعریف هندسی ضرب نقطهای است!
در نهایت با توجه به دو معادله آخر میتوان مشاهده کرد که:
![Rendered by QuickLaTeX.com \[x . y = x_1y_1 + x_2y_2 = \displaystyle\sum_{i=1}^{2} (x_iy_i)\]](https://www.outlier.ir/wp-content/ql-cache/quicklatex.com-1f98246f8932c34794aa63f54257a93c_l3.png)
فرمول بالا نیز تعریف جبری ضرب نقطهای است.
چند جمله در مورد نماد ضرب نقطهای (.)
به این دلیل به این نماد ضرب نقطهای گفته میشود که برای نمایش آن، یک نقطه بین دو بردار گذاشته میشود.
وقتی در مورد ضرب نقطهای x . y صحبت میکنیم مانند این است که درباره مفاهیم زیر صحبت کنیم
- ضرب داخلی
 (در جبر خطی)
(در جبر خطی) - ضرب اسکالر به دلیل این که وقتی ما ضرب دو بردار را انجام میدهیم، یک اسکالر(یک عدد حقیقی) را بر میگرداند.
تصویر عمود یک بردار
با داشتن دو بردار x و y میخواهیم تصویر عمود x بر روی y را پیدا کنیم.
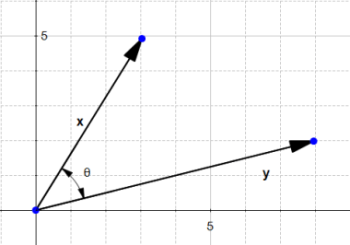
شکل ۱۶
برای این منظور بردار x را روی y تصویر میکنیم
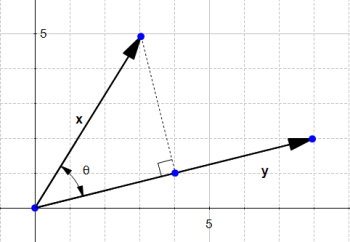
شکل ۱۷
این کار بردار z را به ما خواهد داد
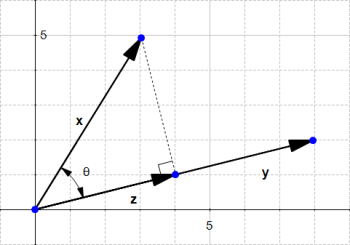
شکل ۱۸ z تصویر x روی y است
طبق تعریف:
![]()
![]()
در مورد ضرب نقطهای در همین بخش دیدیم که
![]()
پس در معادله بالا ![]() را جایگذاری میکنیم:
را جایگذاری میکنیم:
![]()
![]()
اگر بردار u را به عنوان جهت بردار y تعریف کنیم، در این صورت:
![]()
و
![]()
در این صورت راه سادهای برای محاسبه نرم بردار z خواهیم داریم.
از آنجایی که این بردار جهت یکسانی با بردار y دارد، پس آن هم بردار جهت u را خواهد داشت.
![]()
![]()
و میتولن گفت که:
بردار ![]() تصویر بردار x بر روی y است.
تصویر بردار x بر روی y است.
چرا علاقمند شدیم که درباره تصویر عمود بردار بدانیم؟ در مثال ما این بردار به ما این اجازه را میدهد تا فاصله بین x و نقطهای که خط عمود، بردار y را قطع میکند، محاسبه کنیم.
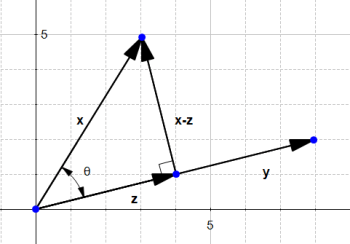
شکل ۱۹
میتوان مشاهده کرد که این فاصله برابر ![]() است.
است.
![]()
ابرصفحه SVM
درک معادله ابرصفحه
به احتمال زیاد از قبل میدانید که معادله یک خط y = ax + b است. با این وجود زمانی که در مورد ابرصفحه مطالعه میکنیم، متوجه میشویم که معادله یک ابرصفحه به صورت زیر تعریف میشود:
![]()
این دو معادله چه شباهتی به هم دارند و چطور باهم مرتبطند؟
در معادله ابرصفحه میتوانید مشاهده کنید که نام متغیرها به صورت ذخیم نوشته شدهاند به این معنی که آنها بردار هستند! علاوه بر این ![]() روشی است که ما ضرب داخلی دو بردار را محاسبه میکنیم و اگر دقت کنید، ضرب داخلی نام دیگر ضرب نقطهای است.
روشی است که ما ضرب داخلی دو بردار را محاسبه میکنیم و اگر دقت کنید، ضرب داخلی نام دیگر ضرب نقطهای است.
توجه کنید که
![]()
را میتوان به این صورت نیز نوشت
![]()
با داشتن دو بردار
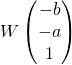
و
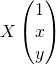
![]()
![]()
دو معادله اخیر در واقع راهای متفاوت نشان دادن یک چیز یکسان هستند.
جالب است که اگر توجه کنیم ![]() همان
همان ![]() است. یعنی این مقدار محل تلاقی خط با محور عمودی را مشخص میکند.
است. یعنی این مقدار محل تلاقی خط با محور عمودی را مشخص میکند.
چرا ما از معادله ابر صفحه ![]() بهجای
بهجای ![]() استفاده میکنیم؟
استفاده میکنیم؟
به دو دلیل:
- برای کار با تعداد بعدهای بیشتر از ۲، استفاده از این فرم برای نمایش سادهتر است.
- بردار w همیشه برای ابرصفحه نرمال خواهد بود.(چون ما از این بردار برای تعریف ابرصفحه استفاده میکنیم. همانطور که در اینجا مشاهده میکنید، زمانی که ما یک ابرصفحه را تعریف میکنیم، فرض میکنیم، برداری که عمود بر ابرصفحه است را از قبل در اختیار داریم. )
و این خاصیت آخر در محاسبه فاصله نقطه از ابرصفحه، مورد استفاده قرار خواهد گرفت.
محاسبه فاصله یک نقطه تا ابرصفحه
در شکل ۲۰ ابرصفحهای را داریم که گروهی از دادهها را تفکیک میکند.
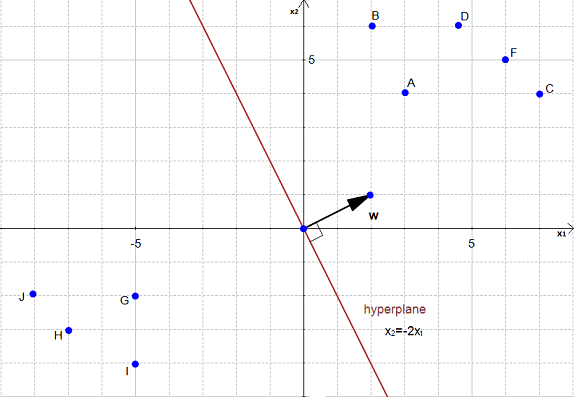
شکل ۲۰
برای سادگی مقدار ![]() را برابر ۰ در نظر میگیریم.
را برابر ۰ در نظر میگیریم.
همانطور که در شکل ۲۰ مشاهده میکنید، معادله ابرصفحه برابر است با:
![]()
که برابر است با
![]()
با پارامترهای:
![]()
و
![]()
توجه کنید که بردار w در شکل ۲۰ نمایش داده شده است. (نقطه w یک قلم داده نیست.)
میخواهیم فاصله بین نقطه ![]() و ابرصفحه را محاسبه کنیم.
و ابرصفحه را محاسبه کنیم.
و این همان فاصله بین A و تصویرش روی ابرصفحه است.
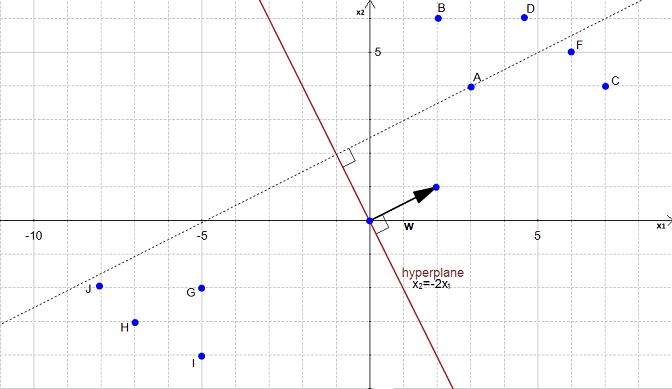
شکل ۲۱
میتوان نقطه A را به صورت برداری نشان داد که ابتذای آن مبدٔ مختصات است.
اگر بردار a را روی بردار نرمال w تصویر کنیم

شکل ۲۲: تصویر a روی w
بردار p به دست خواهد آمد.
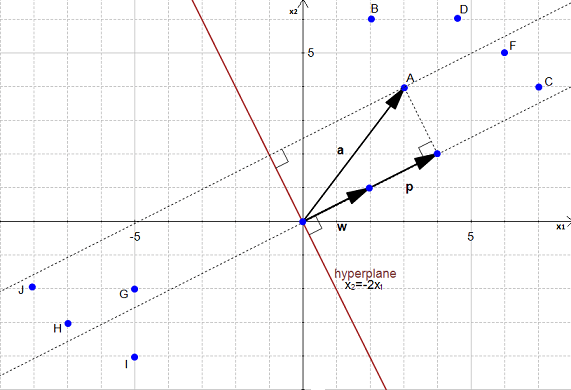
شکل ۲۳: p تصویر بردار a روی w است.
هدف ما پیدا کردن فاصله بین نقطه ![]() و ابرصفحه است.
و ابرصفحه است.
میتوان در شکل ۲۳ مشاهده کرد که این فاصله همان اندازه بردار p (![]() ) است.
) است.
اجازه دهید که این مقدار را محاسبه کنیم.
با دو بردار که نرمال ابرصفحه است و که بردار بین مبدأ مختصات و نقطه A است شروع میکنیم.
![]()
اگر بردار u جهت بردار w باشد
![]()
p تصویر بردار a روی w است. در نتیجه:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
محاسبه حاشیه ابرصفحه
حال که فاصله ![]() بین A و ابرصفحه را داریم، حاشیه به صورت زیر محاسبه میشود:
بین A و ابرصفحه را داریم، حاشیه به صورت زیر محاسبه میشود:
![]()
خب تبریک میگم! حاشیه ابرصفحه را محاسبه کردیم!
نتیجهگیری
این پایان قسمت دوم از آموزش ریاضیات پشت SVM است.
درباره مطالب ریاضی مربوط به این بحث، مطالب بیشتری وجود دارد. اما من امیدوارم که بتوانید باقیمانده مطالب را بدون مشکل دنبال کنید.
بعدش چی؟
حال که یاد گرفتیم چطور حاشیه را محاسبه کنیم، ممکن است که نیاز داشته باشیم تا نحوه انتخاب بهترین ابرصفحه را بدانیم. این مطلب در مقاله SVM – درک مفاهیم ریاضی مورد نیاز – قسمت سوم توضیح داده خواهد شد.

سلام به خاطر مطلب خوب تون بسیار سپاسگزارم.
دو تا سوال دارم
لینک قسمت بعدی این آموزش رو پیدا نکردم.
در نهایت که p به دست اومد چرا حاشیه شد ۲||p|| ؟ عدد ۲ رو متوجه نمی شم؟ ممنون
سلام. خواهش میکنم. ممنون از نظرتون.
قسمتهای بعدی این آموزش رو متأسفانه هتوز فرصت نکردم که بنویسم.
ببینید اندازه |p| در واقع فاصله نزدیکترین نقطه از بین همه نقطهها به ابر صفحه هست. یعنی همین که ما فاصله ۱ نقطه رو پیدا کنیم که به ابر صفحه نزدیکتر باشه این فاصله رو از ابر صفحه ۲ برابر میکنیم که بتونیم اون ۲ خط موازی و یا همون حاشیه رو تشکیل بدیم و در قسمتهای بعدی آموزش سعی میکنیم که مقدار این حاشیه رو تا جایی که ممکن هست افزایش بدیم(فاصله بین ۲ خط موازی).