این قسمت سوم از آموزشهای ریاضی مربوط به ماشینهای بردار پشتیبان است. اگر قسمتهای قبلی را هنوز مطالعه نکردهاید، میتوانید آموزش را از قسمت اول با مطالعه مقاله:SVM – درک مفاهیم ریاضی مورد نیاز – قسمت اول شروع کنید.
اما این مقاله در مورد چیست؟
تمرکز اصلی این مقاله روی نشان دادن منطقی است که به ما اجازه میدهد تا ابرصفحه بهینه را انتخاب کنیم.
در زیر به خلاصهای از مواردی که در ادامه خواهیم دید اشاره شده است:
- چطور میتوان ابرصفحه بهینه را پیدا کرد؟
- چطور فاصله بین دو ابرصفحه را محاسبه کنیم؟
- مسأله بهینهسازی SVM چیست؟
نحوه پیدا کردن ابرصفحه بهینه:
در پایان قسمت دوم فاصله ![]() بین یک نقطه A و ابرصفحه را محاسبه کردیم. پس مقدار حاشیه که برابر با
بین یک نقطه A و ابرصفحه را محاسبه کردیم. پس مقدار حاشیه که برابر با ![]() بود را محاسبه کردیم.
بود را محاسبه کردیم.
با این که آن حاشیه در جدا کردن دادهها، عملکرد خوبی را داشت، ابرصفحه بهینه نبود.
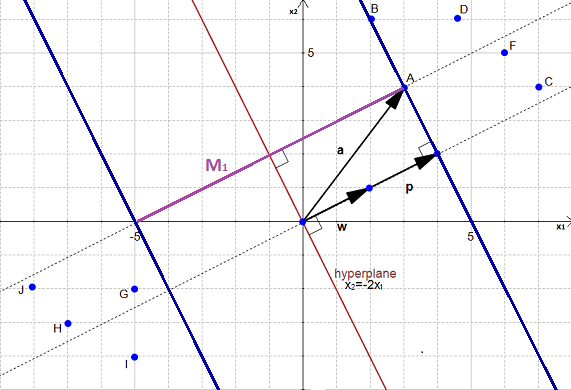
شکل ۱: حاشیهای که در قسمت دوم محاسبه کردیم به صورت M1 نمایش داده شده است.
همانطور که در قسمت اول مشاهده کردیم، ابرصفحهای بهینه است که حاشیه دادههای آموزشی را حداکثر کند.
در شکل ۱ میتوانیم مشاهده کنیم که حاشیه M1 که با ۲ خط آبی رنگ مشخص شده است(بین ۲ خط آبی قرار دارد)، بزرگترین حاشیهای که دادهها را تفکیک میکند نیست. بزرگترین حاشیه M2 است که در شکل ۲ نمایش داده شده است.
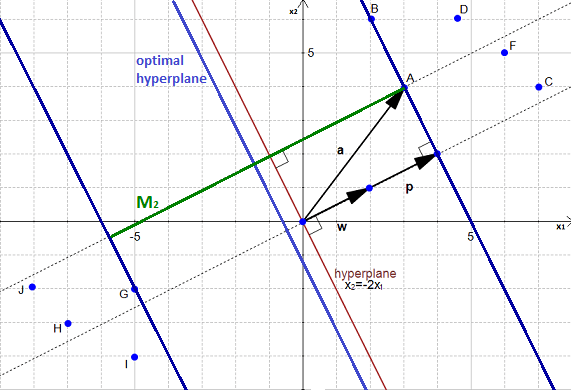
شکل ۲: ابرصفحه بهینه مقداری سمت چپ ابرصفحهای که در قسمت دوم استفاده کردیم قرار دارد.
همچنین شما میتوانید ابر صفحه بهینه را در شکل ۲ مشاهده کنید. این ابر صفحه، سمت چپ ابر صفحه اولیه قرار دارد. (به سادگی میتوان ابر صفحه بهینه یا خطی که از وسط M2 عبور میکند را رسم کرد.)
الآن باید متوجه شده باشید که ابرصفحهها و حاشیهها، ارتباط نزدیکی باهم دارند و درست هم متوجه شدید!
اگر ما ابرصفحهای داشته باشیم، میتواتیم حاشیه آن را باتوجه به تعدادی از دادهها محاسبه کنیم و اگر ما حاشیهای که بین ۲ ابرصفحه است را داشته باشیم (خطهای آبی تیره در شکل ۲)، میتوانیم یک ابرصفحه سومی را پیدا کنیم که دقیقا از وسط حاشیه عبور میکند.
پیدا کردن بزرگترین حاشیه در واقع همان پیدا کردن ابرصفحه بهینه است.
چطور میتوان بزرگترین حاشیه را پیدا کرد؟
این کار نسبتا ساده است:
- شما یک مجموعه داده در اختیار دارید
- دو ابرصفحهای که داده را تفکیک میکند و هیچ نقطهای بین آنها نیست را انتخاب کنید.
- فاصله بین آنها(حاشیه) را به حداکثر برسانید
ناحیه محصور بین دو ابرصفحه، بزرگترین حاشیه موجود خواهد بود.
اگر به همین سادگی هست، پس چطور اغلب در فهمیدن SVM مشکل دارند؟
به این دلیل که معمولا سادگی به مقداری انتزاع و اصطلاحات ریاضی نیاز دارد تا خوب فهمیده شود.
در ادامه این دستورالعمل را قدمبهقدم بررسی خواهیم کرد.
قدم اول: مجموعه دادهای داریم (D) و میخواهیم آن را طبقهبندی کنیم.
بیشتر وقتها داده ما از ![]() بردار
بردار ![]() تشکیل میشوند.
تشکیل میشوند.
به هر ![]() مقداری مانند
مقداری مانند ![]() انتساب داده میشود که مشخص میکند این المان (بردار) متعلق به کلاس
انتساب داده میشود که مشخص میکند این المان (بردار) متعلق به کلاس ![]() است یا کلاس
است یا کلاس ![]() .
.
توجه کنید که ![]() تنها میتواند مقدارهای
تنها میتواند مقدارهای ![]() یا
یا ![]() را داشته باشد.
را داشته باشد.
مورد دیگر اینکه، بیشتر وقتها برای مثال وقتی که میخواهیم طبقهبندی متن را انجام دهیم، بردار ![]() ما دارای تعداد زیادی بعد خواهد بود. پس اگر بردار
ما دارای تعداد زیادی بعد خواهد بود. پس اگر بردار ![]() ،
، ![]() داشته باشد، میتوانیم آن را یک بردار
داشته باشد، میتوانیم آن را یک بردار ![]() -بعدی بنامیم.
-بعدی بنامیم.
پس مجموعه داده شما (D)، یک مجموعه ![]() تایی از زوجهای مرتب
تایی از زوجهای مرتب ![]() است.
است.
تعریف رسمیتر یک مجموعه داده ابتدایی در مجموعه نظریهها به صورت زیر است:
![]()
قدم دوم: ما نیاز داریم که دو ابرصفحه جداکننده که داده را تفکیک کند و دادهای بین آن نباشد را انتخاب کنیم
پیدا کردن دو ابرصفحه که دادهها را از هم تفکیک کند، زمانی که قلم و کاغذ داشته باشیم کار راحتی است، اما با داشتن تعدادی داده p-بعدی، این کار چون چنین خطی را نمیتوانیم رسم کنیم، تبدیل به کار مشکلی میشود.
علاوه بر آن، حتی اگر داده ما ۲-بعدی باشد، پیدا کردن ابرصفحه جداکننده، ممکن نخواهد بود! شما در صورتی میتوانید این ابرصفحه را رسم کنید که داده به صورت خطی تفکیکپذیر باشد.
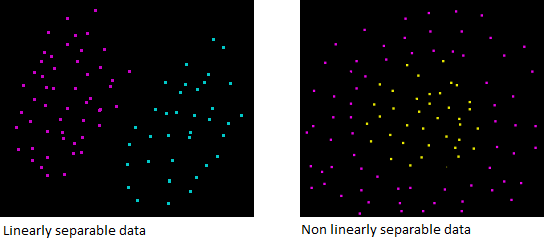
شکل ۳: داده شکل سمت چپ به کمک یک صفحه قابل تفکیک است، درحالی که داده شکل سمت راست اینگونه نیست.
پس فرض کنیم که داده ما D بهصورت خطی تفکیکپذیر باشد. میخواهیم دو ابرصفحه پیدا کنیم که دادهای بین آنها نباشد، اما راهی برای نمایش آنها نداریم.
نگاهی دیگر به معادله ابرصفحه
قبلا دیدیم که معادله ابرصفحه بهصورت زیر میتواند نوشته شود.
![]()
همچنین، در ویکیپدیا مقالهای در مورد ماشین بردار پشتیبان گفتهشده که:
هر ابرصفحه میتواند بهصورت مجموعهای از نقطههای ![]() که در معادله
که در معادله ![]() صدق میکنند، نشان داده شود.
صدق میکنند، نشان داده شود.
اول، علامت دیگری برای ضرب نقطهای میبینیم. در مقاله از ![]() بهجای
بهجای ![]() استفاده شدهاست.
استفاده شدهاست.
ممکن است که تعجب کنید… ![]() از کجا آمده است؟ آیا تعریف قبلی ما نادرست بودهاست؟ جواب خیر است. همهچیز به نحوه استفاده از علامتها برمیگردد. در تعریف ما بردارهای
از کجا آمده است؟ آیا تعریف قبلی ما نادرست بودهاست؟ جواب خیر است. همهچیز به نحوه استفاده از علامتها برمیگردد. در تعریف ما بردارهای ![]() و
و ![]() سه بعد دارند، درحالی که در ویکیپدیا دو بعد دارند:
سه بعد دارند، درحالی که در ویکیپدیا دو بعد دارند:
با داشتن دو بردار سه-بعدی ![]() و
و ![]() داریم:
داریم:
![]()
![]()
با داشتن دو بردار دو-بعدی ![]() و
و ![]() داریم:
داریم:
![]()
![]()
حالا اگر ![]() را به دو طرف معادله (۲) اضافه کنیم خواهیم داشت:
را به دو طرف معادله (۲) اضافه کنیم خواهیم داشت:
![]()
![]()
در ادامه این آموزش از بردارهای دو-بعدی استفاده خواهیم کرد.(مانند معادله (۲)).
با داشتن ابرصفحه ![]() که داده را تفکیک و در معادله زیر صدق میکند:
که داده را تفکیک و در معادله زیر صدق میکند:
![]()
میتوانیم دو ابرصفحه دیگر مثل ![]() و
و ![]() که آنها هم داده را تفکیک میکنند و دارای معادله زیر هستند را انتخاب کنیم:
که آنها هم داده را تفکیک میکنند و دارای معادله زیر هستند را انتخاب کنیم:
![]()
و
![]()
در نتیجه فاصله ![]() از
از ![]() و
و ![]() برابر است.
برابر است.
همچنین در اینجا متغیر ![]() ضروری نیست، پس ما میتوانیم برای سادهتر شدن مسأله،
ضروری نیست، پس ما میتوانیم برای سادهتر شدن مسأله، ![]() در نظر بگیریم.
در نظر بگیریم.
![]()
و
![]()
حال میخواهیم مطمئن شویم که نقطهای(دادهای) بین آنها نیست.
ما هر ابرصفحهای را انتخاب نمیکنیم. تنها آنهایی را انتخاب میکنیم که از قیدهای(محدودیتهای) زیر پیروی میکنند:
برای هر بردار ![]() :
:
![]() برای
برای ![]() هایی که دارای کلاس ۱ هستند
هایی که دارای کلاس ۱ هستند
یا
![]() برای
برای ![]() هایی که دارای کلاس ۱- هستند
هایی که دارای کلاس ۱- هستند
درک قیدها (محدودیتها)
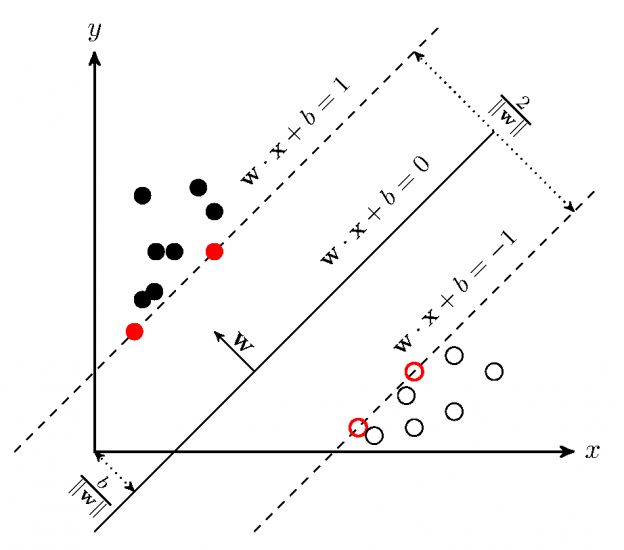
در شکلهای زیر، نقطههای قرمز متعلق به کلاس ۱ و نقطههای آبی متعلق به کلاس ۱- هستند.
به شکل ۴ توجه کنید و نقطه A را در نظر بگیرید. رنگ آن قرمز است، پس متعلق به کلاس ۱ است و ما باید از اینکه قید ![]() را نقض نکند، اطمینان حاصل کنیم.
را نقض نکند، اطمینان حاصل کنیم.
زمانی که ![]() باشد، میبینیم که نقطه روی ابرصفحه وجود دارد. پس
باشد، میبینیم که نقطه روی ابرصفحه وجود دارد. پس ![]() و قید مسأله نیز نقض نشده است. همین عبارت برای نقطه B هم صادق است.
و قید مسأله نیز نقض نشده است. همین عبارت برای نقطه B هم صادق است.
زمانی که ![]() باشد، میبینیم که نقطه در بالای ابرصفحه است. پس
باشد، میبینیم که نقطه در بالای ابرصفحه است. پس ![]() و قید مسأله نیز نقض نشده است. همین عبارت برای نقطههای G, F, E, و D نیز صادق است.
و قید مسأله نیز نقض نشده است. همین عبارت برای نقطههای G, F, E, و D نیز صادق است.
به دلیلهای مشابه، متوجه خواهیم شد که قید دوم نیز برای کلاس -۱ صادق است.
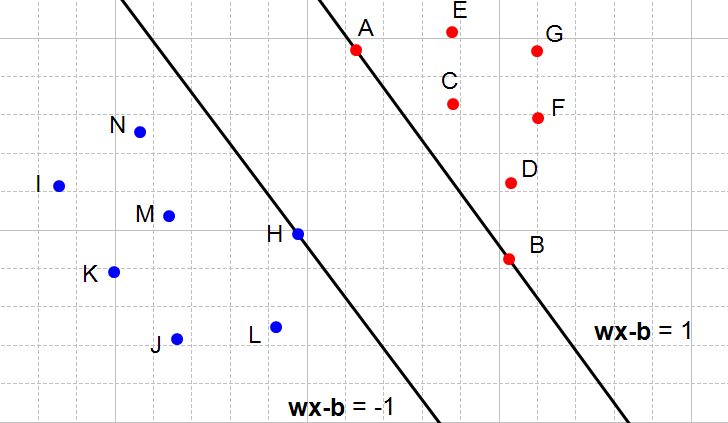
شکل ۴: دو ابرصفحه با توجه به قیدهای مسأله
در شکل ۵ یک جفت ابرصفحه دیگر را با توجه به قیدهای مسأله را مشاهده میکنیم:
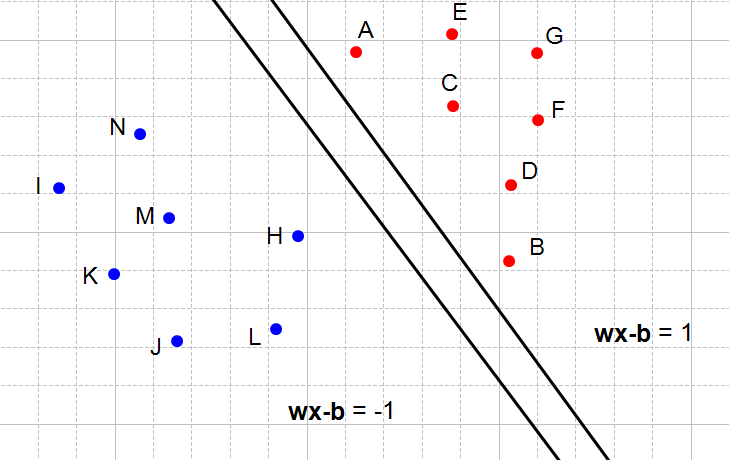
شکل ۵: دو ابرصفحه دیگر با توجه به قیدهای مسأله
حال موردهایی را ارزیابی میکنیم که قیدهای مسأله را نقض میکنند:
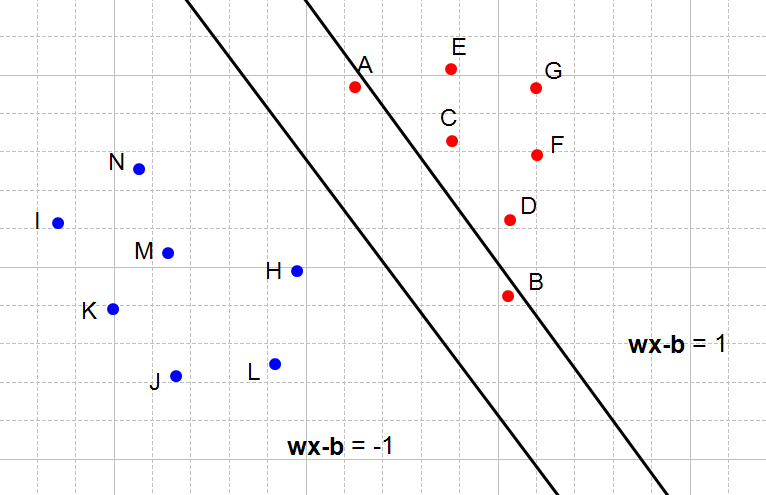
شکل ۶: ابرصفحه سمت راست قید اول مسأله را نقض میکند
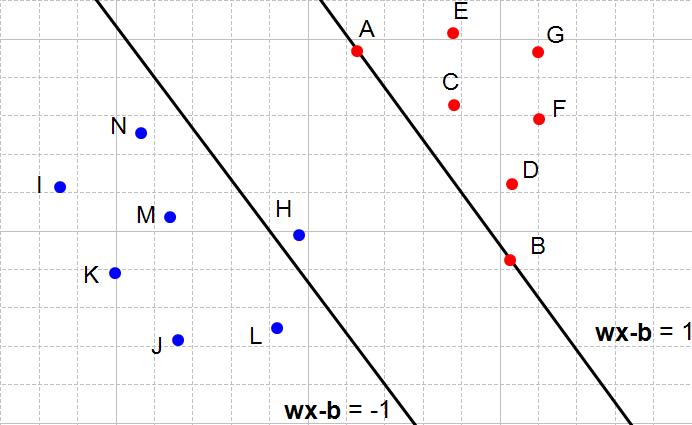
شکل ۷: ابرصفحه سمت چپ قید دوم مسأله را نقض میکند
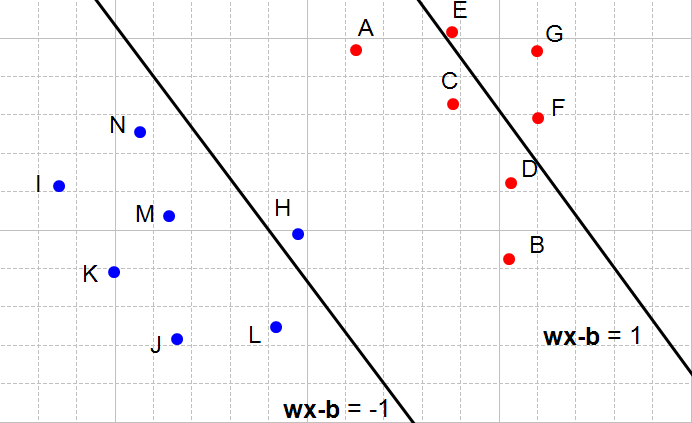
شکل ۸: هر دو قید مسأله نقض شدهاند
ولی این که قید مسأله نقض شود به چه معنی هست؟ به این معنی که ما نمیتوانیم این دو ابرصفحه را انتخاب کنبم. در این حالت میتوانیم مشاهده کنیم که هربار قیدها نقض شدهاند (شکل ۶، ۷ و ۸) نقطههای بین ابرصفحهها قرار گرفتهاند.
با تعریف کردن این قیدها، راهی پیدا کردیم که به هدف اولیه که همان انتخاب دو ابرصفحه بدون نقطهای بین آنها بود، برسیم و این نه تنها برای مثالهای ما بلکه برای فضاهای p-بعدی هم کار میکند!
ترکیب هر دو قید
در ریاضی، همه دوست دارند که چیزها را به صورت ساده نمایش دهند.
معادلههای (۴) و (۵) میتوانند به صورت یک قید تکی باهم ترکیب شوند:
با معادله (۵) شروع میکنیم
برای ![]() که دارای کلاس ۱- هستند
که دارای کلاس ۱- هستند
![]()
و ضرب هر دو طرف آن در ![]() (که همیشه در این معادله برابر ۱- است)
(که همیشه در این معادله برابر ۱- است)
![]()
که یعنی معادله (۵) میتواند به صورت زیر نوشته شود:
![]() برای
برای ![]() هایی که دارای کلاس ۱- هستند
هایی که دارای کلاس ۱- هستند
در معادله (۴) چون ![]() علامت نامساوی را تغییر نمیدهد.
علامت نامساوی را تغییر نمیدهد.
![]() برای
برای ![]() هایی که دارای کلاس ۱ هستند
هایی که دارای کلاس ۱ هستند
معادلههای (۶) و (۷) را ترکیب میکنیم:
![]() برای همه
برای همه ![]()
حال بهجای دو قید (معادلههای ۴ و ۵)، یک قید واحد (معادله ۸) را داریم، ولی آنها از نظر ریاظی مساوی هستند. پس اثر آنها نیز مثل هم است (هیچ نقطهای بین دو ابرصفحه نخواهد بود).
قدم سوم: بیشینه کردن فاصله بین دو ابرصفحه
این احتمالا مشکلترین قسمت مسأله است. ولی جای نگرانی نیست، همه چیز را توضیح خواهم داد.
الف) فاصله بین دو ابرصفحه چقدر است؟
قبل از سعی کردن برای بیشینه کردن فاصله بین ۲ ابرصفحه، باید از خودمان بپرسیم که چطور باید این کار را انجام دهیم؟
فرض کنیم:
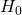 ابرصفحهای با معادله
ابرصفحهای با معادله 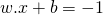 باشد
باشد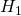 ابرصفحهای با معادله
ابرصفحهای با معادله 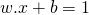 باشد
باشد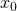 یک نقطه روی ابرصفحه
یک نقطه روی ابرصفحه 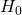 باشد
باشد
m را فاصله خط عمود از ![]() تا ابرصفحه
تا ابرصفحه ![]() مینامیم. بنا به تعریف، m چیزی است که ما آن را حاشیه مینامیم.
مینامیم. بنا به تعریف، m چیزی است که ما آن را حاشیه مینامیم.
و چون ![]() روی
روی ![]() است، m همان فاصله بین ابرصفحههای
است، m همان فاصله بین ابرصفحههای ![]() و
و ![]() است.
است.
حال سعی خواهیم کرد که مقدار m را پیدا کنیم.
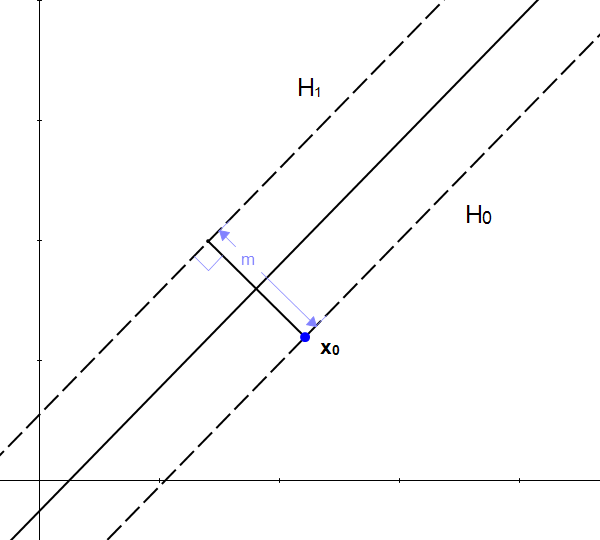
شکل ۹: m فاصله بین دو ابرصفحه است
ممکن است فکر کنید که اگر m را ![]() اضافه کنیم، نقطه دیگری به دست خواهد آمد و این نقطه روی ابرصفحه دیگر خواهد بود!
اضافه کنیم، نقطه دیگری به دست خواهد آمد و این نقطه روی ابرصفحه دیگر خواهد بود!
ولی این ایده کار نخواهد کرد. دلیلش هم این است که m یک اسکالر و ![]() یک بردار است و به همین دلیل جمع این دو باهم امکانپذیر نیست. میدانیم که جمع دو بردار امکانپذیر است، پس اگر m را به فرم یک بردار در بیاوریم، میتوانیم آنها را باهم جمع کنیم.
یک بردار است و به همین دلیل جمع این دو باهم امکانپذیر نیست. میدانیم که جمع دو بردار امکانپذیر است، پس اگر m را به فرم یک بردار در بیاوریم، میتوانیم آنها را باهم جمع کنیم.
میتوانیم مجموعهای از نقطهها را پیدا کنیم که در فاصله m از ![]() باشند. این را میتوان بهصورت یک دایره نمایش داد.
باشند. این را میتوان بهصورت یک دایره نمایش داد.
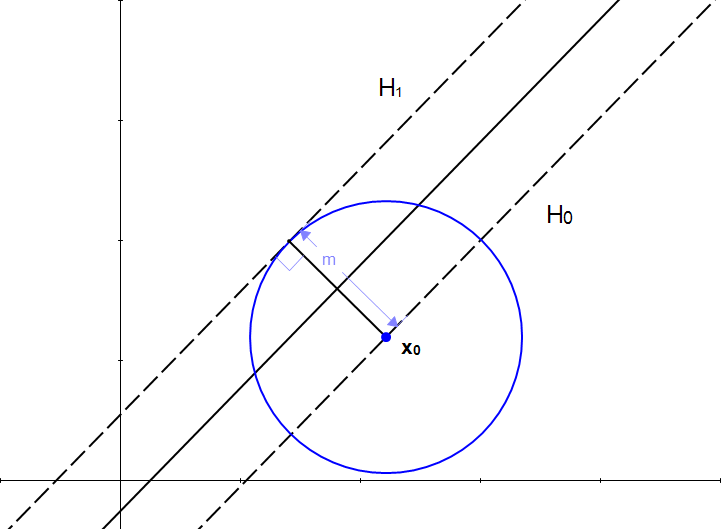
شکل ۱۰: همه نقطههای روی دایره، در فاصله m از ![]() قرار دارند
قرار دارند
با مشاهده عکس ضرورت تبدیل کردن به بردار مشخص خواهد شد. ما فقط طول m را محاسبه کردیم و هنوز یک مورد مهم دیگر را نداریم: جهت. (با توجه به قسمت دوم، هر بردار یک جهت و یک اندازه دارد).
ما نمیتوانیم یک اسکالر را با یک بردار جمع کنیم، ولی میدانیم که اگر یک اسکالر را در یک بردار ضرب کنیم، بردار دیگری به دست خواهد آمد.
با توجه به صورت مسأله، برداری که ما درنظر داریم:
- دارای اندازه m است
- بر ابرصفحه
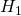 عمود است
عمود است
خوشبختانه از قبل یک بردار عمود بر ![]() را داریم و آن هم w است. (به این دلیل که
را داریم و آن هم w است. (به این دلیل که ![]() است)
است)
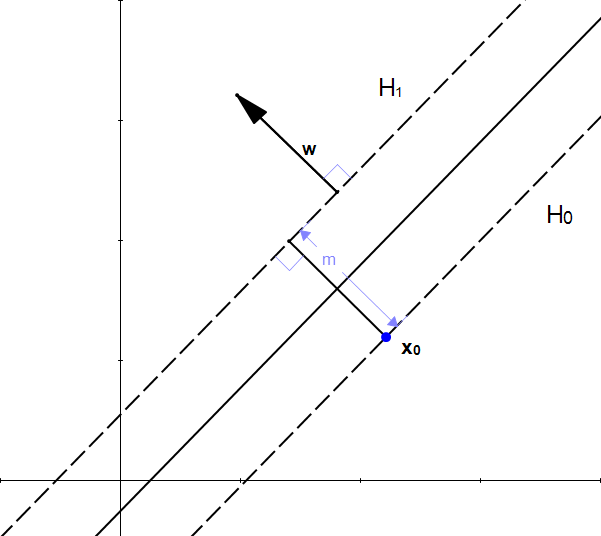
شکل ۱۱: w بر ابرصفحه ![]() عمود است
عمود است
![]() را بردار واحد w تعریف میکنیم. از آنجایی که این یک بردار واحد است:
را بردار واحد w تعریف میکنیم. از آنجایی که این یک بردار واحد است: ![]() و هم جهت با بردار w است، پس آن هم بر ابرصفحه عمود است.
و هم جهت با بردار w است، پس آن هم بر ابرصفحه عمود است.
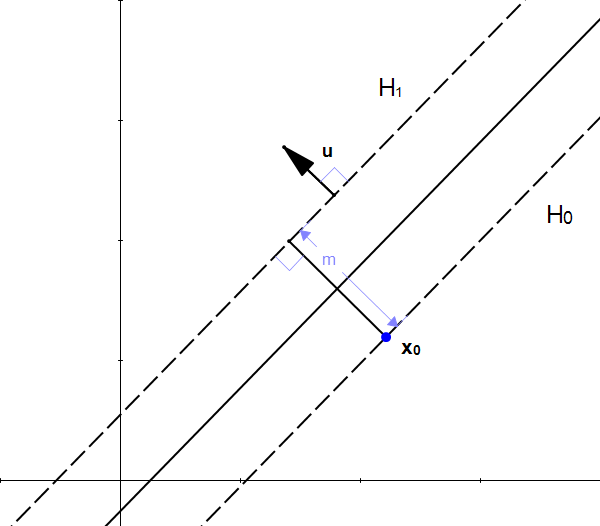
شکل ۱۲: u نیز بر ابرصفحه ![]() عمود است
عمود است
اگر u را در w ضرب کنیم، بردار ![]() به دست میآید و:
به دست میآید و:
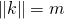
- k بر ابرصفحه
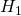 عمود است (چون با u همجهت است)
عمود است (چون با u همجهت است)
با توجه به این خاصیتها میتوانیم مشاهده کنیم k برداری است که دنبال آن میگشتیم.
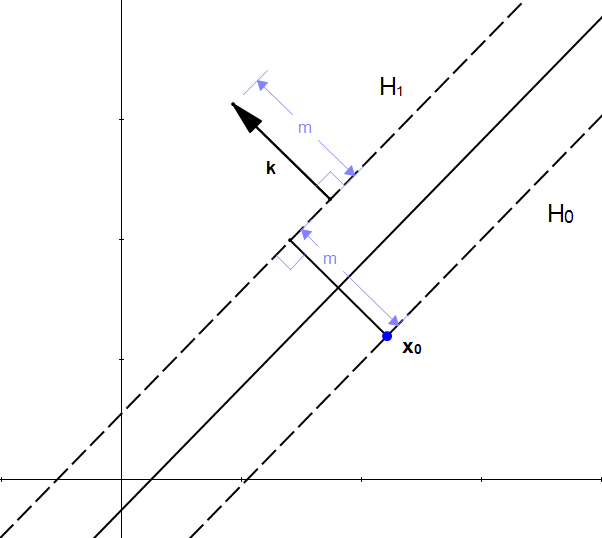
شکل ۱۳: k برداری به طول m و عمود بر ابرصفحه ![]() است
است
![]()
انجام شد! اسکالر m را به بردار k تبدیل کردیم که میتوانیم از آن استفاده کنیم تا عمل جمع با بردار ![]() را انجام دهیم.
را انجام دهیم.
اگر از نقطه ![]() شروع کنیم و مقدار k را به آن اضافه کنیم، نقطه
شروع کنیم و مقدار k را به آن اضافه کنیم، نقطه ![]() به دست میآید که روی ابرصفحه
به دست میآید که روی ابرصفحه ![]() قرار دارد و در شکل ۱۴ نمایش دادهشده است.
قرار دارد و در شکل ۱۴ نمایش دادهشده است.
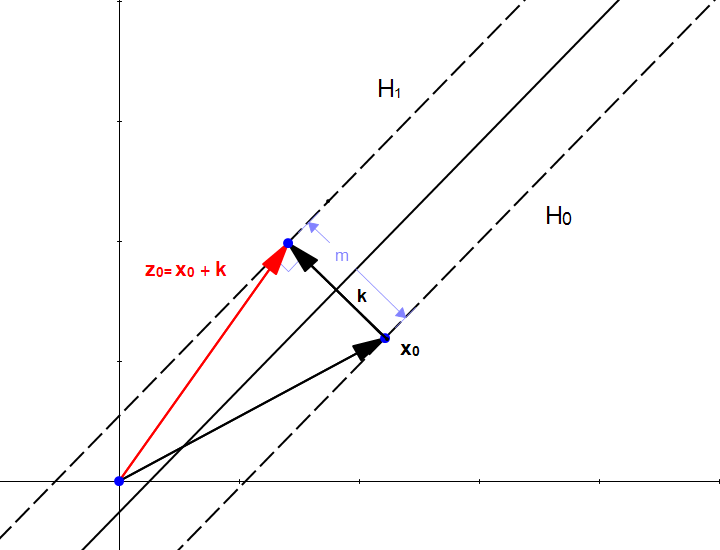
شکل ۱۴: ![]() یک نقطه روی
یک نقطه روی ![]() است
است
این واقعیت که ![]() روی
روی ![]() است، همچنین به معنی عبارت زیر است:
است، همچنین به معنی عبارت زیر است:
![]()
میتوانیم ![]() را با
را با ![]() جایگزین کنیم.
جایگزین کنیم.
![]()
میتوانیم k را با استفاده از معادله (۹) جایگزین کنیم
![]()
حال معادله (۱۲) را باز میکنیم
![]()
ضرب نقطهای یک بردار در خودش، برابر با مربع اندازهاش است. پس:
![]()
![]()
![]()
چون ![]() روی
روی ![]() است، پس:
است، پس: ![]()
![]()
![]()
![]()
به این ترتیب راهی برای محاسبه m پیدا کردیم.
ب) چطور فاصله بین دو ابرصفحه را بیشینه کنیم
حال فرمولی برای محاسبه حاشیه داریم:
![]()
تنها متغیری که در این فرمول میتوانیم تغییر دهیم، اندازه w است.
این فرمول را برای مقدارهای مختلف بررسی میکنیم:
- زمانی که
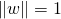 باشد،
باشد، 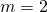 است
است - زمانی که
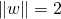 باشد،
باشد، 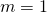 است
است - زمانی که
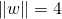 باشد،
باشد، 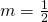 است
است
میتوان مشاهده کرد که اندازه (نرم) بیشتر، مقدار حاشیه کمتر را به همراه خواهد داشت.
بیشینه کردن حاشیه درواقع همان کمینه کردن نرم w است
هدف ما به حداکثر رساندن مقدار حاشیه است. در میان همه ابرصفحههای ممکن که قیدهای مسأله را رعایت میکنند، ابرصفحهای با کوچکترین ![]() را انتخاب میکنیم، به این دلیل که بیشترین حاشیه را خواهد داشت،
را انتخاب میکنیم، به این دلیل که بیشترین حاشیه را خواهد داشت،
این برای ما مسأله بهینهسازی زیر را به وجود میآورد:
کمینه کردن با توجه به (w, b)
![]()
با توجه به ![]()
(برای هر ![]() )
)
حل این مسأله مشابه حل کردن یک معادله است. زمانی که آن را حل کردیم، زوج (w, b) را برای ![]() خواهیم داشت که کوچکترینمقدار ممکن است و همچنین قیدهای مسأله نیز درنظر گرفته خواهند شد. و این یعنی معادله ابرصفحه بهینه را خواهیم داشت!
خواهیم داشت که کوچکترینمقدار ممکن است و همچنین قیدهای مسأله نیز درنظر گرفته خواهند شد. و این یعنی معادله ابرصفحه بهینه را خواهیم داشت!
نتیجهگیری
تا الآن فهمیدیم که برای پیدا کردن ابرصفحه بهینه، باید یک مسأله بهینهسازی را حل کنیم. مسألههای بهینهسازی ذاتا پیچیده هستند و برای حل آنها به اطلاعات و پیشزمینه قبلی نیاز است. پس ما قدم به قدم پیش خواهیم رفت و درباره مسألههای کمینه کردن بدون قید در قسمت چهارم مطالعه خواهیم کرد.