SVM – درک مفاهیم ریاضی مورد نیاز – قسمت چهارم

این قسمت چهارم از آموزش‌ مفاهیم ریاضی پشت ماشین‌های بردار پشتیبان است. در این پست نحوه حل کردن مسأله کمینه‌سازی بدون قید را یاد می‌گیریم.

اگر قسمت‌های قبلی را هنوز مطالعه نکرده‌اید، می‌توانید آموزش را از قسمت اول با مطالعه مقاله:SVM – درک مفاهیم ریاضی مورد نیاز – قسمت اول شروع کنید.

درباره این قسمت

نوشتن این قسمت به دلیل گسترده بودن موضوع و دانش اولیه زیادی که نیاز دارد، زمان زیادی را از من گرفت. این که چه مطلب‌هایی را باید توضیح دهم و از روی چه مطلب‌هایی باید رد شوم هم تصمیم سختی بود. پس از مدتی با یک پست طولانی مواجه شدم که مطالعه آن مشکل میشد. برای همین تصمیم گرفتم که این پست را به چند قسمت تقسیم کنم. پس به قسمت‌های ۴، ۵ و ۶ خوش‌آمدید و خوش خواهید آمد! 🙂

در این پست سعی شده که مطلب‌ها تا حد ممکن برای همه ساده باشند، ولی با این وجود من نمی‌توانم که همه چیز را کامل توضیح دهم. برای همین من فرض می‌کنم که شما از قبل با مشتق‌ها و مشتق‌های جزیی آشنایی دارید. همچنین انتظار می‌رود که شما ماتریس و ترانهاده ماتریس را بشناسید و نحوه محاسبه دترمینان ماتریس را نیز بدانید.

در طول چند ماه گذشته، من نظرها و تشویق‌های زیادی را دریافت کردم. خیلی‌ها هم زمان انتشار این پست و بقیه قسمت‌ها را پیگیری کرده‌اند. همین‌جا از همه شما تشکر می‌کنم و امیدوارم که از آموزش‌ها لذت ببرید.

جایی که مسأله را رها کردیم

در قسمت سوم, متوجه شدیم که برای به حداکثر رساندن مقدار حاشیه، باید اندازه (نرم) $w$ را به حداقل برسانیم.

این یعنی ما باید مسأله بهینه‌سازی زیر را حل کنیم:

کمینه کردن با توجه به (w, b)

$\|w\|$

با توجه به $y_i(w.x_i+b) \geq 1$

(برای هر $i=1, ..., n$ )

اولین نکته‌ای که درباره این مسأله بهینه‌سازی باید به آن توجه کنیم این است که این مسأله دارای قیدهایی هست. این قیدها در خطی که با عبارت «با توجه به» شروع می‌شود تعریف شده‌اند. ممکن است که شما فکر کنید، فقط یک قید داریم، ولی درواقع $n$ قید داریم. (به دلیل وجود عبارت «به ازای هر» در خط آخر)

“خیلی خب، چطور باید این مسأله را حل کنیم؟ (به احتمال زیاد زمان زیادی را منتظر پاسخ این سؤال بوده‌اید!!!)”

قبل از دست و پنجه نرم کردن با چنین مسأله پیچیده‌ای، اجازه دهید که با یک مسأله ساده‌تر شروع کنیم. اول باید ببینیم که یک مسأله بهینه‌سازی بدون قید را باید حل کرد، یا به‌طور دقیق‌تر کمینه‌سازی بدون قید را فرا خواهیم گرفت. این همان مسأله پیدا کردن ورودی‌ای است که باعث می‌شود تابع، کم‌ترین مقدار خودش را تولید کند و یا برگرداند. (توجه کنید که در مورد SVM، مایل هستیم تابعی که نرم (اندازه) $w$ را محاسبه می‌کند، کمینه کنیم. می‌توانیم این تابع را $f$ بنامیم و آن را به صورت $f(w) = \|w\|$ بنویسیم.)

حداقل‌سازی بدون قید

اجازه دهید نقطه $x^*$ را در نظر بگیریم. (شما باید این را “x ستاره” بخوانید، ما فقط یک ستاره به آن اضافه کردیم که بدانید درباره یک متغیر خاص صحبت می‌کنیم نه درباره هر x)

چطور بدانیم که $x^*$ یک مینیمم محلی تابع $f$ است؟ خب این تقریبا ساده است. ما فقط نیاز داریم که قضیه زیر را اعمال کنیم:

قضیه:

$f:\Omega \to R$ تابعی است پیوسته و مشتق‌پذیر که مشتق دوم آن در $x^*$ موجود است.

اگر $x^*$ در رابطه $\nabla f(x^*) = 0$ صدق کند و $\nabla ^2 f(x^*)$ همیشه مثبت باشد، در این صورت $x^*$ یک مینیمم محلی است.

حقیقت تلخی که در این قضیه وجود دارد این است که با وجود مختصر بودن، فهمیدن آن بدون داشتن مقداری اطلاعات و دانش قبلی، تقریبا غیرممکن است. $\nabla f(x^*) = 0$ چیست؟ $\nabla ^2 f(x^*)$ چیست؟ منظور از همیشه مثبت چیست؟

در بعضی از موارد اطلاعات بیشتری به ما داده خواهد شد و به کمک ‌آن‌ها، قضیه قبل می‌تواند به صورت زیر نوشته شود:

قضیه (با جزییات بیشتر):

اگر $x^*$ صدق کند:

۱. $f$ یک گرادیان صفر در $x^*$ دارد:

$\nabla f(x^*) = 0$

۲. Hessian $f$ در $x^*$ همیشه مثبت است:

$z^T ((\nabla ^2 f(x^*)) z> 0, \forall z \in R^n$

جایی که:

$\nabla ^2 f(x) = \begin{pmatrix} \frac{\delta ^2 f}{\delta x_1 ^2} & \cdots & \frac{\delta ^2 f}{\delta x_1 \delta x_n} \\ \vdots & \ddots & \vdots \\ \frac{\delta ^2 f}{\delta x_n \delta x_1} & \cdots & \frac{\delta ^2 f}{\delta x_n ^2} \end{pmatrix}$

در این صورت $x^*$ یک مینیمم محلی است.

همه این‌ها به چه معنی هستند؟

اجازه دهید که این تعریف را قدم به قدم ارزیابی کنیم.

قدم اول:

$f:\Omega \to R$ که تابعی است پیوسته و مشتق‌پذیر که مشتق دوم آن در $x^*$ موجود است را در نظر بگیرید.

اول تابعی که آن را $f$ می‌نامیم را معرفی می‌کنیم. این تابع مقدارهایش را از مجموعه $\Omega$ (امگا) می‌گیرد . یک مقدار حقیقی را برمی‌گرداند. اولین سختی که در این‌جا وجود دارد این هست که ما نمی‌توانیم مقدار $\Omega$ را مشخص کنیم ولی مقدار آن را در خط بعدی حدس بزنیم. این تابع $f$ باید پیوسته باشد و مشتق دوم آن نیز موجود باشد و در غیر این صورت ادامه تعریف نادرست خواهد بود.

قدم دوم:

$x^*$ یک مینیمم محلی است، اگر و فقط اگر:

می‌خواهیم مقداری را پیدا کنیم که وقتی آن را به $f$ می‌دهیم، کم‌ترین مقدار خود را تولید کند. ما این مقدار را به طور ساده $x^*$ می‌نامیم.

از این علامت دو چیز را می‌توانیم نتیجه بگیریم:

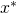$x^*$ به صورت ضخیم (Bold) نوشته شده است. پس این یک بردار است. این یعنی 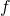$f$ یک تابع چند متغیره است.
در نتیجه مجموعه 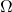$\Omega$ که پیش‌تر آن را دیده‌ایم، مجموعه‌ای است که ما مقدارهایی از آن را به 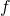$f$ می‌دهیم. این یعنی مجموعه 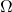$\Omega$ مجموعه‌ای از بردارها است و 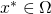$x^* \in \Omega$ (“x ستاره امگا (Omega) تعلق دارد”).

قدم سوم:

$f$ یک گرادیان صفر در $x^*$ دارد.

اگر بخواهیم $x^*$ یک مینیمم محلی $f(x)$ باشد. این اولین شرطی است که باید در نظر بگیریم. ما باید بررسی کنیم که گرادیان تابع $f$ در $x^*$ برابر با صفر باشد. گرادیان چیست؟ این اسم را فقط به عنوان یک مشتق در نظر بگیرید.

تعریف: “گرادیان یک فرم کلی‌تر از مفهوم مشتق یک تابع در یک بعد از چند بعد است.” (ویکی‌پدیا)

این تعریف به ما قسمتی از اطلاعات مورد نیاز را می‌دهد. گرادیان در حقیقت همان مشتق است. اما برای تابع‌هایی مثل $f$ ، بردارها را به عنوان ورودی می‌گیرد. برای همین است که ما نیاز داریم تا در درجه اول تابع $f$ مشتق‌پذیر باشد. اگر این‌طور نباشد نمی‌توانیم گرادیان را محاسبه کنیم و ادامه دهیم.

در محاسبات، زمانی که ما می‌خواهیم یک تابع را بررسی کنیم، معمولا علامت مشتق آن را بررسی می‌کنیم. این به ما اجازه می‌دهد که صعودی یا نزولی بودن و همچنین مینیمم و ماکزیمم تابع را مشخص کنیم. با برابر کردن مشتق با صفر می‌توانیم نقطه‌های بحرانی تابع که در آن‌ها به حداکثر و حداقل خود می‌رسد را پیدا کنیم. (توجه: برای تابع‌هایی که متغیرهای بیشتری دارند، باید مشتق‌های جزیی را در این نقطه برابر صفر قرار دهیم.)

گرادیان یک تابع با علامت $\nabla$ (nabla) نمایش داده می‌شود.

عبارت

$\nabla f(x^*) = 0$

فقط یک بیان دیگر از “ $f$ در $x^*$ گرادیان صفر دارد” به کمک علامت‌های ریاضی است.

برای بردار $x^* (x_1 , x_2 , x_3)$ ، $\nabla f(x^*) =0$ یعنی:

$\frac{\delta f}{\delta x_1}(x^*) = 0$

$\frac{\delta f}{\delta x_2}(x^*) = 0$

$\frac{\delta f}{\delta x_3}(x^*) = 0$

قدم چهارم:

ماتریس Hessian تابع $f$ در $x^*$ همیشه مثبت است.

این جایی هست که بیشتر مردم گیج می‌شوند. این جمله به تنهایی نیاز به مقدار زیادی پیش‌زمینه دارد. شما باید موارد زیر را بدانید:

ماتریس Hessian یک ماتریس از مشتق‌های مرتبه دوم است.
چطور می‌توان همیشه مثبت بودن یک ماتریس را مشخص کرد؟

ماتریس Hessian

ماتریس Hessian یک ماتریس است و فقط یک اسم به آن نسبت داده‌ایم. می توانستیم آن را H بنامیم ولی در عوض برای صراحت بیشتر، آن را $\nabla ^2 f(x)$ می‌نامیم. ما همان سمبل $\nabla$ که برای گرادیان استفاده کردیم را نگه داشتیم و به آن یک $^2$ اضافه کرده‌ایم که نشان دهیم این بار درباره مشتق‌های جزیی مرتبه دوم صحبت می‌کنیم. سپس به تابعی که این مشتق‌ها را محاسبه می‌کند نام $f$ را اختصاص می‌دهیم. با نوشتن $f(x)$ می‌دانیم که $f$ یک بردار $x$ را به عنوان ورودی می‌گیرد و ماتریس Hessian برای $x$ داده شده محاسبه می‌شود.

جمع‌بندی: ما باید ماتریسی به نام Hessian را برای $x^*$ محاسبه کنیم.

پس ما با داشتن تابع $f$ و مقدار $x^*$ همه سلول‌های ماتریس را به وسیله فرمول زیر محاسبه می‌کنیم:

در نهایت ما ماتریس Hessian را خواهیم داشت که حاوی همه عددهایی است که محاسبه کرده‌ایم.

اجازه دهید نگاهی به تعریف بیاندازیم تا مطمئن شویم که آن را خوب متوجه شده‌ایم.

تعریف: در ریاضی ماتریس Hessian یا Hessian یک ماتریس مربعی از مشتق‌های جزیی مرتبه دوم یک تابع با مقدارهای اسکالر است. این ماتریس انحنای محلی تابعی از چند متغیر را توصیف می کند. (ویکی‌پدیا)

(توجه: یک تابع با مقدار اسکالر، تابعی است که یک یا چند مقدار را می‌گیرد ولی فقط یک مقدار را برمی‌گرداند. در مورد ما $f$ یک تابع اسکالر است.)

همیشه مثبت

حال که ماتریس Hessian را داریم، می‌خواهیم بدانیم که آیا در $x^*$ همیشه مثبت است؟

تعریف: یک ماتریس متقارن $A$ همیشه مثبت است اگر به ازای همه $x \in R^n$ $x^T Ax > 0$ باشد. (منبع)

این بار قبل از هرچیز، یک‌بار دیگر به تعریف داده شده توجه می‌کنیم. خواندن آن ممکن است به دلیل استفاده از علامت‌های ریاضی، کمی مشکل باشد. اگر ما جای $A$ را با $\nabla ^2 f(x^*)$ عوض کنیم، دقیقا به همان فرمول قسمت دوم می‌رسیم. از قضیه با جزییات بیشتر می‌دانیم:

$z^T ((\nabla ^2 f(x^*)) z> 0, \forall z \in R^n$

مشکل این تعریف این است که درباره ماتریس متقارن صحبت می‌کند. یک ماتریس متقارن یک ماتریس مربعی است که با ترانهاده خود برابر باشد.

ماتریس Hessian مربعی است، ولی آیا متقارن هم هست؟

از شانس خوب ما بله!

“اگر مشتق‌های دوم $f$ همگی در همسایگی $D$ پیوسته باشند، در نتیجه Hessian $f$ یک ماتریس متقارن در محدوده بازه $D$ دارد.” (ویکی‌پدیا)

اما حتی با تعریف، ما هنوز نمی‌دانیم که چطور همیشه مثبت بودن Hessian را بررسی کنیم. این به خاطر فرمول $z^T ((\nabla ^2 f(x^*))z\geq 0$ برای همه $z$ در $R^n$ است.

ما نمی‌توانیم که این فرمول را برای همه مقدارهای $z$ در $R^n$ امتحان کنیم!

برای همین از قضیه زیر استفاده می‌کنیم:

قضیه:

جمله‌های زیر با هم برابرند:

ماتریس متقارن 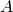$A$ همیشه مثبت است.
همه eigenvalueهای 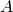$A$ مثبت هستند.
همه leading principal minorهای 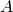$A$ مثبت هستند.
ماتریس nonsingular مربعی 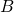$B$ به قسمی که 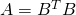$A=B^T B$ وجود دارد. (منبع)

پس ما سه راه داریم که همیشه مثبت بودن یک ماتریس را بررسی کنیم:

به وسیله محاسبه eigenvalueهای آن و بررسی این که آن‌ها مثبت هستند.
به وسیله محاسبه leading principal minorهای آن و بررسی این که آن‌ها مثبت هستند.
به وسیله پیدا کردن یک ماتریس مربعی nonsingular $B$ به قسمی که $A=B^T B$ .

اجازه دهید از روش دوم استفاده کنیم و آن را با جزییات بیشتر بررسی کنیم.

محاسبه leading principal minors (کهاد)

Minors

برای محاسبه $M_{ij}$ سطر $i$ و ستون $j$ را حذف می‌کنیم و دترمینان باقی‌مانده ماتریس را محاسبه می‌کنیم.

مثال:

ماتریس ۳*۳ زیر را در نظر بگیرید:

$\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix}$

برای محاسبه Minor $M_{}$ 12 این ماتریس، سطر شماره ۱ و ستون شماره ۲ را حذف می‌کنیم. بنابراین خواهیم داشت:

$\begin{pmatrix} \Box & \Box & \Box \\ d & \Box & f \\ g & \Box & i \end{pmatrix}$

سپس دترمینان ماتریس زیر را محاسبه می‌کنیم:

$\begin{pmatrix} d & f \\ g & i \end{pmatrix}$

که برابر است با: $di - fg$

Principal minors

یک minor $M_{ij}$ زمانی که $i=j$ باشد، principal minor نامیده می‌شود.

برای ماتریس ۳*۳ ما، principal minorها به صورت زیر هستند:

$M_{11} = ei -fh$
$M_{22} = ai -cg$
$M_{33} = ae-bd$

هنوز تمام نشده! در واقع minorها همچنین دارای چیزی که ما آن را مرتبه می‌نامیم هستند.

تعریف:

یک minor $A$ از مرتبه $k$ اگر با حذف کردن $n-k$ سطر و $n-k$ ستون با شماره‌های یکسان به دست بیاید، principal است. (منبع)

در مثال قبل، ماتریسی که استفاده شد ۳*۳ بود. پس $n=3$ است و ما ۱ سطر را حذف کردیم، در نتیجه ما minorهای مرتبه دوم را محاسبه کردیم.

$\binom{n}{k}$ $\Box$ principal minor مرتبه $k$ وجود دارد و ما هر یک از آن‌ها را با $\Delta k$ نمایش می‌دهیم.

برای جمع‌بندی:

$\Delta 0$ : وجود ندارد، زیرا اگر ما سه سطر و سه ستون را حذف کنیم، در واقع کل ماتریس را حذف کرده‌ایم.

$\Delta 1$ : $(3-1)=2$ سطر و ۲ ستون با شماره یکسان را حذف می‌کنیم.

پس ما سطرهای ۱ و ۲ و ستون‌های ۱ و ۲ را حذف می‌کنیم.

$\begin{pmatrix} \Box & \Box & \Box \\ \Box & \Box & \Box \\ \Box & \Box & i \end{pmatrix}$

این یعنی یک principal minor از مرتبه ۱، $i$ است. اجازه دهید که بقیه را نیز پیدا کنیم:

سطرهای ۲ و ۳ و ستون‌های ۲ و ۳ را حذف می‌کنیم و $a$ به دست می‌آید.
سطرهای ۱ و ۳ و ستون‌های ۱ و ۳ را حذف می‌کنیم و $e$ به دست می‌آید.

$\Delta 2$ : همان چیزی است که قبلا آن را دیده‌ایم:

$M_{11} = ei -fh$
$M_{22} = ai -cg$
$M_{33} = ae-bd$

$\Delta 3$ : چیزی را حذف نمی‌کنیم. پس این همان دترمینان ماتریس است: $aei+bfg+cdh-ceh-bdi-afh$

Leading principal minor (کهاد)

تعریف:

کهاد $A$ از مرتبه $k$ همان minor از مرتبه $k$ است که از حذف کردن $n-k$ سطر و ستون آخر به دست آمده است.

در نتیجه این موضوع به دست آوردن کهاد را ساده‌تر خواهد کرد. اگر ما $D_k$ را برای کهاد از مرتبه $k$ بنویسیم، متوجه خواهیم شد که:

$D_1 = a$ (دو سط و ستون آخر را حذف کرده‌ایم)

$D_2 = ae-bd$ (سطر آخر و ستون آخر را حذف کرده‌ایم)

$D_3 = aei+bfg + cdh -ceg - bdi -afh$

حال که همه کهادهای ماتریس را محاسبه کرده‌ایم، می‌توانیم آن‌ها را به ازای ماتریس Hessian $x^*$ محاسبه کنیم و اگر همه آن‌ها مثبت باشند، متوجه خواهیم شد که ماتریس همیشه مثبت است.

حال که ما هر آنچه که نیاز داریم را می‌دانیم را کاملا ارزیابی کردیم و شما قادر هستید که راه حل یک مسأله کمینه‌سازی بدون قید را درک کنید، اجازه دهید که با یک مثال بررسی کنیم که تا الآن این همه چیز را به خوبی متوجه شده‌اید.

مثال:

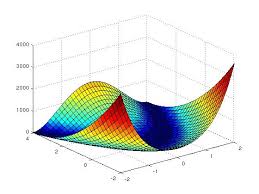
در این مثال سعی خواهیم کردکه مقدار حداقل تابع $f(x,y)=(2-x)^2 + 100(y-x^2)^2$ که با نام تابع موزی روزنبروک (Rosenbrock’s banana function) شناخته می‌شود را پیدا کنیم.

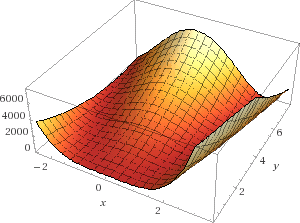
تابع روزنبروک به ازای $a=2$ و $b=100$

اول، به دنبال نقطه‌هایی که $\Delta f(x,y)$ را برابر با صفر می‌کنند خواهیم گشت.

$\Delta f(x,y) = \begin{pmatrix} \frac{\delta f}{\delta x} \\ \frac{\delta f}{\delta y} \\ \end{pmatrix}$

بنابراین مشتق‌های جزیی را محاسبه می‌کنیم:

$\frac{\delta f}{\delta x} = 2(200x^3 - 200xy + x -2)$

$\frac{\delta f}{\delta y} = 200(y-x^2)$

(راهنمایی: اگر می‌خواهید از درستی محاسبات خود مطمئن شوید، می‌توانید از ابزار Wolfram alpha استفاده کنید.)

هدف ما پیدا کردن حالتی است که پاسخ هر دو معادله، برابر با صفر می‌شود، پس ما نیاز داریم تا دستگاه معادلات زیر را حل کنیم:

$2(200x^3 -200xy+x-2) = 0 \quad(1)$

$200(y-x^2) = 0 \quad(2)$

اگر معادله را باز کنیم، خواهیم داشت:

$400x^3 -400xy + 2x -4 =0 \quad(3)$

$200y -200x^2 = 0 \quad(4)$

معادله (۲) را در $2x$ ضرب می‌کنیم:

$400xy - 400x^3 = 0 \quad(5)$

حال معادله (۳) و (۵) را باهم جمع می‌کنیم:

$400x^3-400xy+2x-4+400xy-400x^3 = 0 \quad(6)$

که به صورت زیر ساده می‌شود:

$2x-4=0$

$x=2$

$x$ را در معادله شماره (۴) جایگذاری می‌کنیم

$200y-200 \times 2^2 = 0$

$200y-800=0$

$y= \frac{800}{200}$

$y=4$

به نظر می‌رسد که ما نقطه $(x,y)=(2,4)$ که در $\nabla f(x,y) = 0$ صدق می‌کند را پیدا کرده‌ایم.

ماتریس Hessian برابر است با:

$\nabla ^2 f(x, y) = \begin{pmatrix} \frac{\delta ^2 f}{\delta x^2} & \frac{\delta ^2 f}{\delta xy} \\ \frac{\delta ^2 f}{\delta yx} & \frac{\delta ^2 f}{\delta y^2} \end{pmatrix}$

$\frac{\delta ^2 f}{\delta x^2} = 1200x^2 - 400y +2$

$\frac{\delta ^2 f}{\delta xy} = -400x$

$\frac{\delta ^2 f}{\delta yx} = -400x$

$\frac{\delta ^2 f}{\delta y^2} = 200$

حال اجازه دهید Hessian را برای $(x,y)=(2,4)$ محاسبه کنیم

$\nabla ^2 f(x,y) = \begin{pmatrix} 3202 & -800 \\ -800 & 200 \end{pmatrix}$

ماتریس متقارن است. می‌توانیم کهادهای آن را بررسی کنیم:

Minorهای مرتبه اول:

اگر ما سطر و ستون آخر را حذف کنیم، $M_{11}$ برابر ۳۲۰۲ خواهد بود.

Minorهای مرتبه دوم:

این همان دترمینان ماتریس Hessian است:

$3202 * 200 - (-800) \times (-800) = 400$

همه کهادهای Hessian مثبت هستند. این یعنی Hessian همیشه مثبت است.

دو شرطی که لازم داشتیم، برآورده شده و می‌توانیم نتیجه بگیریم که نقطه $(2,4)$ یک مینیمم محلی است.

مینیمم محلی؟

به یک نقطه، کمینه محلی گفته می‌شود زمانی که کوچک‌ترین مقدار در یک بازه باشد. به صورت رسمی‌تر:

با داشتن تابع $f$ که در دامنه $X$ تعریف شده باشد، نقطه $x^*$ کمینه محلی است اگر یک $\epsilon > 0$ وجود داشته باشد که برای هر $x$ در بازه $X$ در فاصله $\epsilon$ از $x^*$ ، $f(x^*) \leq f(x)$ باشد. این موضوع در شکل زیر نشان داده شده است.

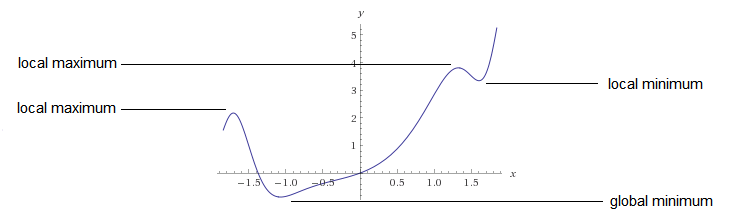
همچنین یک مینیمم سراسری، در تمام بازه دامنه تابع صحیح است.

با داشتن تابع $f$ که در دامنه $X$ تعریف شده است، نقظه $x^*$ کمینه سراسری است اگر:

$f(x^*) \leq f(x)$ برای همه xهای موجود در $X$

همه سختی کار ما، فقط پیدا کردن مینیمم محلی بود، ولی در زندگی واقعی، ما معمولا می‌خواهیم مینیمم سراسری را پیدا کنیم…

مینیمم سراسری را چطور پیدا کنیم؟

یک راه ساده برای پیدا کررن مینیمم سراسری وجود دارد:

همه مینیمم‌‌های محلی را پیدا کنید
کوچک‌ترین آن‌ها را بیابید و این همان مینیمم سراسری است.

یک رویکرد دیگر مطالعه تابعی است که قصد کمینه کردن آن را داریم. اگر این تابع محدب باشد، مطمئن هستیم که مینیمم محلی آن، همان مینیمم سراسری است.

نتیجه‌گیری

دیدیم که پیدا کردن مینیمم یک تابع، خیلی هم کار ساده‌ای نیست و تازه این به معنی پیدا کردن مینیمم سراسری هم نبود. با این حال، کار کردن با بعضی از تابع‌ها که محدب نامیده می‌شوند، ساده‌تر است. تابع محدب چیست؟ قسمت پنجم این آموزش را مطالعه فرمایید تا جواب این سؤال را پیدا کنید! ممنون که تا این‌جا با من بودید.

اشتراک‌گذاری

لایه‌های مخفی یک داده پرت

روزنوشته‌های یک علاقمند به یادگیری انسان، ماشین و علم داده

SVM – درک مفاهیم ریاضی مورد نیاز – قسمت چهارم

درباره این قسمت

جایی که مسأله را رها کردیم

حداقل‌سازی بدون قید

قضیه:

قضیه (با جزییات بیشتر):

همه این‌ها به چه معنی هستند؟

قدم اول:

قدم دوم:

قدم سوم:

قدم چهارم:

ماتریس Hessian

همیشه مثبت

قضیه:

محاسبه leading principal minors (کهاد)

Minors

Principal minors

تعریف:

Leading principal minor (کهاد)

تعریف:

مثال:

Minorهای مرتبه اول:

Minorهای مرتبه دوم:

مینیمم محلی؟

مینیمم سراسری را چطور پیدا کنیم؟

نتیجه‌گیری

دیدگاهتان را بنویسید لغو پاسخ