این قسمت ششم از آموزش مفاهیم ریاضی پشت ماشینهای بردار پشتیبان است. در این پست درباره دوگان، مسألههای بهینهسازی و ضریبهای لاگرانژ یاد میگیریم.
اگر قسمتهای قبلی را هنوز مطالعه نکردهاید، میتوانید آموزش را از قسمت اول با مطالعه مقاله:SVM – درک مفاهیم ریاضی مورد نیاز – قسمت اول شروع کنید.
دوگان
در تئوری بهینهسازی ریاضی، دوگان به این معنی است که به مسألههای بهینهسازی می توان از دو زاویه نگاه کرد، خود مسأله یا دوگان مسأله (اصل دوگان). حل مسأله دوگان، حل مسأله دوگان، یک حد پایین برای راه حل مسأله اصلی (کمینهسازی) فراهم میکند. (ویکیپدیا)
اگر بدانید که حد پایین چیست، درک مفهوم دوگان برای شما بسیار ساده خواهد بود.
حد پایین چیست؟
اگر یک مجموعه پاره مرتب (partially ordered) ![]() (مجموعهای که المانهای قابل مقایسه داشته باشد و در آن رابطه کمتر یا مساوی بتواند استفاده شود.) داشته باشید، حد پایین یک المان از
(مجموعهای که المانهای قابل مقایسه داشته باشد و در آن رابطه کمتر یا مساوی بتواند استفاده شود.) داشته باشید، حد پایین یک المان از ![]() است که کمتر یا مساوی هر المان از
است که کمتر یا مساوی هر المان از ![]() باشد.
باشد.
جهت انتزاع کمتر (کلی گویی). اگر یک عدد حقیقی (از یک مجموعه پاره مرتب ![]() ) انتخاب کنیم و آن از هر المان زیر مجموعهای از
) انتخاب کنیم و آن از هر المان زیر مجموعهای از ![]() کمتر یا مساوی باشد، در این صورت میتوانید آن المان را حد پایین بنامید.
کمتر یا مساوی باشد، در این صورت میتوانید آن المان را حد پایین بنامید.
مثال:
اجازه دهید زیر مجموعهای از ![]() را در نظر بگیریم:
را در نظر بگیریم:
![]()
- چون ۱ کمتر یا مساوی ۲، ۴، ۸ و ۱۲ است، میتوان گفت که ۱ حد پایین
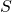 است.
است. - برای مثال همین جمله برای -۳ هم صحیح است.
- وحتی اگر آن در
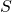 هم باشد، میتوان ۲ را حد پایین
هم باشد، میتوان ۲ را حد پایین 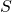 نامید.
نامید.
علاوه بر آن، چون ۲ بزرگتر از هر حد پایین دیگری است، میتوانیم یک اسم خاص به آن اختصاص بدهیم و آن را infimum (بزرگترین حد پایین) مینامیم.
پس در مثال ما، میتوان بینهایت حد پایین انتخاب کرد ولی فقط یک infimum وجود دارد.
توجه: منطق یکسانی برای رابطه “بزرگتر یا مساوی” اعمال میشود و مفهوم حد بالا (upper-bound) و سوپریمم (supremum) را خواهیم داشت.
برگردیم به دوگان
حال که میدانیم حد پایین چیست، از تعریف دوگان چه چیزی را میفهمیم؟ خب این تعریف به این معنی است که اگر یک مسأله کمینهسازی داشته باشیم، میتوانیم همچنین آن را به صورت یک مسأله بیشینهسازی در نظر بگیریم و زمانی که ماکزیمم این مسأله را پیدا کنیم میتواند حد پایین در حل مسأله کمینهسازی باشد و همیشه کمتر یا مساوی مینیمم مسأله کمینهسازی است.
چرا دوگان برای ما مهم است؟
در بعضی از موارد، حل کردن دوگان مسأله سادهتر از حل کردن خود مسأله است.طبق مطلبهایی که درباره حدهای پایین دیدیم، میتوانیم ببینیم که برای بعضی از مسألههای بهینهسازی، حل کردن دوگان مسأله به ما همان نتیجه حل کردن مسأله اصلی را میدهد! ولی چه زمانی؟
عکس زیر را در نظر بگیرید.
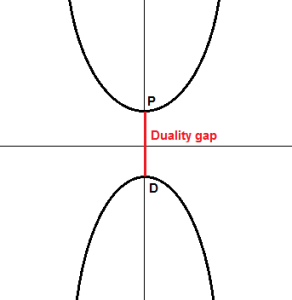
در شکل بالا، تصور کنید که در مسأله اصلی، ما سعی داریم که تابع بالایی را کمینه کنیم. کمینه آن نقطه ![]() است. اگر به دنبال تابع دوگان باشیم، میتوانیم این کار از طریق تابع پایین نمودار انجام دهیم که ماکزیمم آن نقطه
است. اگر به دنبال تابع دوگان باشیم، میتوانیم این کار از طریق تابع پایین نمودار انجام دهیم که ماکزیمم آن نقطه ![]() است. در این مورد میتوانیم به طور واضح مشاهده میکنیم که
است. در این مورد میتوانیم به طور واضح مشاهده میکنیم که ![]() حد پایین است. مقدار
حد پایین است. مقدار ![]() را تعریف میکنیم و به آن فاصله دوگان میگوییم. در این مثال،
را تعریف میکنیم و به آن فاصله دوگان میگوییم. در این مثال، ![]() و به آن دوگان ضعیف (weak duality holds) میگوییم.
و به آن دوگان ضعیف (weak duality holds) میگوییم.
در شکل زیر، مشاهده میکنیم که ![]() ، فاصله دوگان وجود ندارد و به آن دوگان قوی (strong duality holds) میگوییم.
، فاصله دوگان وجود ندارد و به آن دوگان قوی (strong duality holds) میگوییم.
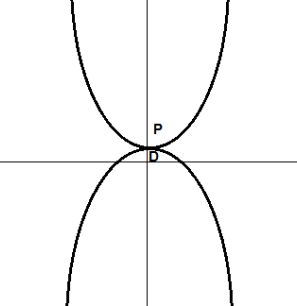
مسألههای بهینهسازی با قید
نشانهگذاری (نماد، علامت)
یک مسأله بهینهسازی معمولا به صورت زیر نوشته میشود:
![]()
![]()
![]()
این نشانهگذاری، فرم استاندارد نام دارد. البته نشانهگذاریهای دیگری نیز وجود دارد.
در این نشانهگذاری، ![]() تابع هدف نامیده میشود (همچنین تابع هزینه هم نامیده میشود). با تغییر
تابع هدف نامیده میشود (همچنین تابع هزینه هم نامیده میشود). با تغییر ![]() (متغیر بهینهسازی) امیدواریم مقدار
(متغیر بهینهسازی) امیدواریم مقدار ![]() را به گونهای پیدا کنیم که مینیمم آن باشد.
را به گونهای پیدا کنیم که مینیمم آن باشد.
همچنین به تعداد ![]() تابع
تابع ![]() وجود دارند که قیدهای تساوی و
وجود دارند که قیدهای تساوی و ![]() تابع
تابع ![]() وجود دارند که قیدهای نامساوی را تعریف میکنند.
وجود دارند که قیدهای نامساوی را تعریف میکنند.
مقدارهایی که ما پیدا کنیم، باید این قیدها را در نظر بگیرند!
در نظر گرفتن قیدها به چه معنی است؟
تصور کنید که سعی در حل کردن مسأله بهینهسازی زیر دارید:
![]()
قیدی وجود ندارد، پس پیدا کردن مینیمم آسان خواهد بود. تابع ![]() زمانی که
زمانی که ![]() باشد برابر ۰ است. این با یک ستاره قرمز روی نمودار شکل زیر نشان داده شده است.
باشد برابر ۰ است. این با یک ستاره قرمز روی نمودار شکل زیر نشان داده شده است.
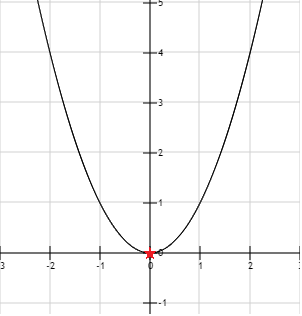
زمانی که قیدی نداشته باشیم، مینیمم برابر ۰ است.
قیدهای تساوی
با این حال، اگر سعی کنیم که یک قید تساوی اضافه کنیم چه میشود؟ برای مثال، میخواهیم که مینیمم را پیدا کنیم ولی باید مطمئن شویم که ![]() . این به این معنی است که ما باید مسأله بهینهسازی زیر را حل کنیم:
. این به این معنی است که ما باید مسأله بهینهسازی زیر را حل کنیم:
![]()
![]()
اینبار زمانی که سعی کنیم ![]() قرار دهیم، میبینیم که تابع مینیمم خودش را بر میگرداند، با این حال نمیتوانیم بگوییم که این راهحل مسأله بهینهسازی ما است. به علاوه، قید
قرار دهیم، میبینیم که تابع مینیمم خودش را بر میگرداند، با این حال نمیتوانیم بگوییم که این راهحل مسأله بهینهسازی ما است. به علاوه، قید ![]() هم نقض شده است. در این مثال، تنها انتخاب ما، استفاده از
هم نقض شده است. در این مثال، تنها انتخاب ما، استفاده از ![]() است و این درواقع همان راه حل است.
است و این درواقع همان راه حل است.
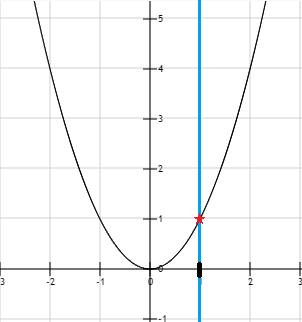
با یک قید تساوی ![]() ، مینیمم برابر ۱ است
، مینیمم برابر ۱ است
با نگاه به این مثال، ممکن است حس کنید که قیدهای تساوی بهدردنخور هستند. چون بیشتر مسألههای بهینهسازی، بیشتر از یک بعد را در نظر میگیرند، این تفکر صحیح نیست.
قیدهای نامساوی
چه میشود اگر الآن از یک قید نامساوی استفاده کنیم؟ این کار ما را با مسألهای به فرم زیر روبرو میکند:
![]()
![]()
این بار، میتوانیم مقدارهای بیشتری از ![]() را امتحان کنیم. برای مثال،
را امتحان کنیم. برای مثال، ![]() قید را در نظر میگیرد، پس میتواند راه حل بالقوه مسأله باشد. در آخر مشاهده میکنیم که تابع
قید را در نظر میگیرد، پس میتواند راه حل بالقوه مسأله باشد. در آخر مشاهده میکنیم که تابع ![]() با توجه به قید مسأله، مینیمم خودش را باز هم در
با توجه به قید مسأله، مینیمم خودش را باز هم در ![]() دارد.
دارد.

قید نامساوی
در نمودار بالا، ناحیه جواب که به صورت سیاه و ضخیم نشان داده شده است، مجموعهای از مقدارهای ![]() است که مجازیم از آنها استفاده کنیم. این مجموعه همچنین مجموعه پاسخ نامیده میشود.
است که مجازیم از آنها استفاده کنیم. این مجموعه همچنین مجموعه پاسخ نامیده میشود.
در نشانهگذاری ریاضی میتوانیم آن را به صورت زیر بنویسیم:
![]()
![]() مجموعهای از مقدارها است که قیدها را در نظر میگیرند.
مجموعهای از مقدارها است که قیدها را در نظر میگیرند.
ترکیب قیدها
میتوان چندین قید به یک مسأله بهینهسازی اضافه کرد. در اینجا مثالی با دو قید نامساوی به همراه نمایش بصری آن داریم:
![]()
![]()
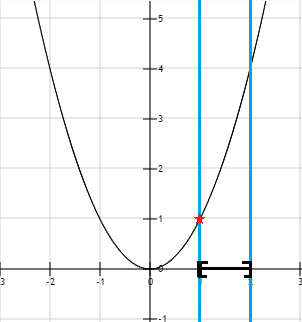
قیدهای مرکب ناحیه پاسخ را محدود میکنند
توجه کنید که همچنین میتوانیم قیدهای تساوی و نامساوی را با هم ترکیب کنیم. تنها محدودیت این است که اگر از قیدهای نقض کننده استفاده کنیم، با مسألهای روبرو میشویم که مجموعه پاسخ ندارد:
![]()
![]()
به علاوه برای این که یک قید در نظر گرفته شود، باید درست باشد. زمانی که چندین قید داشته باشیم، همه آنها باید درست باشند. در مثال بالا، غیر ممکن است که همزمان ![]() برابر با ۱ و کمتر یا مساوی ۰ باشد.
برابر با ۱ و کمتر یا مساوی ۰ باشد.
برای تابع ![]() با یک قید تساوی
با یک قید تساوی ![]() و یک قید نامساوی
و یک قید نامساوی ![]() ، مجموعه جواب برابر است با:
، مجموعه جواب برابر است با:
![]()
راه حل یک مسأله بهینهسازی چیست؟
مقدار بهینه ![]() برای یک مسأله بهینهسازی:
برای یک مسأله بهینهسازی:
![]()
![]()
![]()
عبارت بالا میگوید: اساسا در علامتگذاری ریاضی، مقدار بهینه با در نظر گرفتن همه قیدها،همان اینفیمم ![]() است.
است.
چطور راه حل یک مسأله بهینهسازی با قید را پیدا کنیم؟
از ضریبهای لاگرانژ استفاده میکنیم. این متد توسط ریاضیدان ایتالیایی، ژوزف لوییز لاگرانژ در سال سال ۱۸۰۶ میلادی ابداع شد.

ژوزف لوییز لاگرانژ
ضریبهای لاگرانژ
مثل همیشه میتوانیم یک تعریف خیلی واضح روی ویکیپدیا پیدا کنیم:
در بهینهسازی ریاضی، متد ضرائب لاگرانژ یک استراتژی برای پیدا کردن ماکزیمم و مینیمم تابع با توجه به قیدهای تساوی است. (ویکیپدیا)
یک مورد حساس و قابل توجه در این تعریف این است که ضریبهای لاگرانژ فقط در مورد قیدهای تساوی صحیح هستند. در نتیجه میتوانیم از آنها استفاده کنیم تا بعضی از مسألههای بهینهسازی (آنهایی که یک یا چند قید تساوی دارند) را حل کنیم.
ولی نگران نباشید، ضریبهای لاگرانژ همچنین پایه مورد استفاده در حل مسألههایی با قیدهای نامساوی هستند. پس بد نیست که این مسأله سادهتر را درک کنیم 🙂
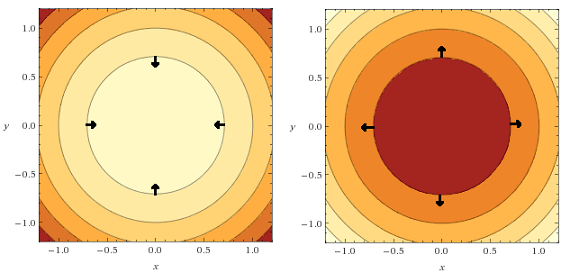
قبل از توضیح ضریبهای لاگرانژ، اجازه دهید که ذهنمان را برای خطهای کانتور (contour lines) آماده کنیم.
خطهای کانتور
مهم است که خطهای کانتور را بفهمیم تا ضریبهای لاگرانژ را بهتر درک کنیم.
نمودار کانتور راهی برای مصورسازی تابع سه-بعدی در دو بعد است.
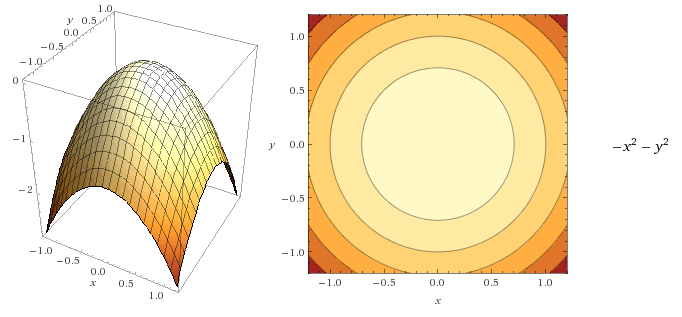
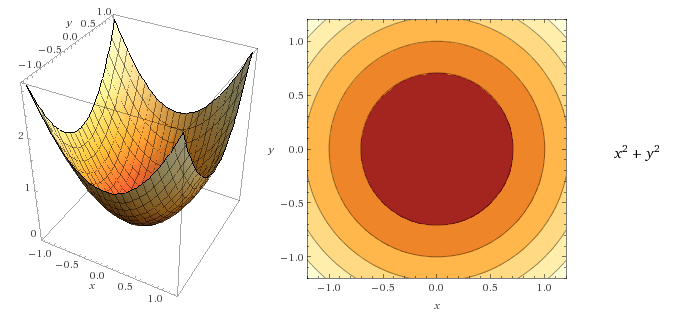
برای مثال: عکس زیر تابع ![]() را در سه بعد (سمت چپ) و با یک نمودار کانتور (سمت راست) نشان میدهد.
را در سه بعد (سمت چپ) و با یک نمودار کانتور (سمت راست) نشان میدهد.
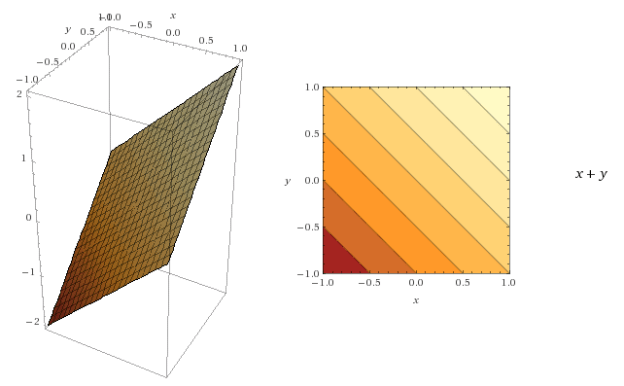
مفاهیم کلیدی در رابطه با خطهای کانتور:
- برای هر نقطه روی خط، تابع یک مقدار یکسان را بر میگرداند.
- محدوده تاریکتر، کوچکترین مقدار تابع است.
میتوانیم آخرین نقطه نمایش داده شده در دو شکل زیر را مشاهده کنید. حتی اگر خط یکسانی داشته باشند، تغییر رنگ به ما اجازه میدهد تا تصویر سه-بعدی تابع را در ذهنمان تصور کنیم.
به علاوه، گرادیان تابع میتواند به صورت یک ناحیه برداری با یک پیکان که به جهت افزایش تابع اشاره میکند نشان داده باشد.
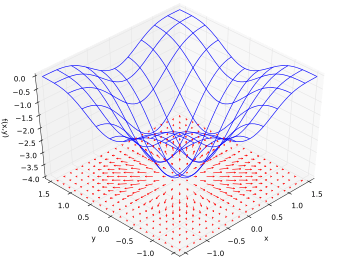
گرادیان تابع به صورت یک ناحیه برداری تصویر شده است (ویکیپدیا)
معلوم میشود که به راحتی میتوانیم بردارهای گرادیان را روی نمودار کانتور رسم کنیم:
- آنها به خط کانتور عمود هستند
- آنها باید به جهت افزایش تابع اشاره کنند. (جهتی که تابع در آن افزایش پیدا میکند)
در شکلهای زیر نمایش آنها روی دو نمودار کانتور را میبینیم:
برگردیم به ضریبهای لاگرانژ
مسأله بهینهسازی زیر را در نظر بگیرید:
![]()
![]()
تابع هدف ![]() و تابع قید
و تابع قید ![]() میتوانند به صورت کانتور در شکلهای زیر نمایش داده شوند:
میتوانند به صورت کانتور در شکلهای زیر نمایش داده شوند:
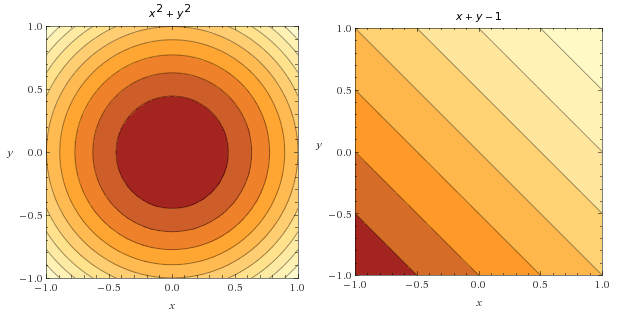
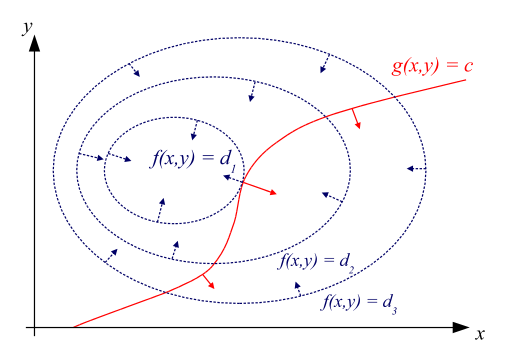
جالب است که به این نکته توجه کنیم که میتوانیم هر دو نمودار کانتور را ترکیب کنیم تا چگونگی رفتار هر دو تابع را روی یک نمودار مصورسازی کنیم. در زیر میتوانید مشاهده کنید که تابع قید با خطهای آبی نمایش داده شده است.
همچنین تعدادی بردار گرادیان از تابع هدف (مشکی) و تعدادی بردار گرادیان از تابع قید (سفید) رسم می کنیم.
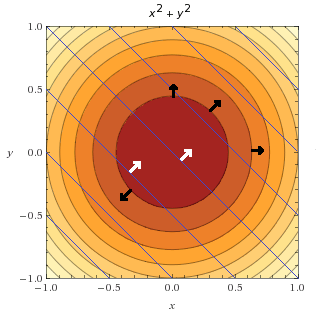
با این حال ما علاقهای به کل تابع قید نداریم. ما قفط به نقطههایی علاقهمندیم که قیدها در آنها رعایت شده باشند. مثال: ![]() .
.
این یعنی ما نقطههایی را میخواهیم که:
![]()
![]()
![]()
در شکل زیر، ما فقط خط ![]() را در بالای تابع هدف رسم میکنیم. قبلا دیدیم که این تابع همچنین مجموعه پاسخ نامیده میشود.
را در بالای تابع هدف رسم میکنیم. قبلا دیدیم که این تابع همچنین مجموعه پاسخ نامیده میشود.
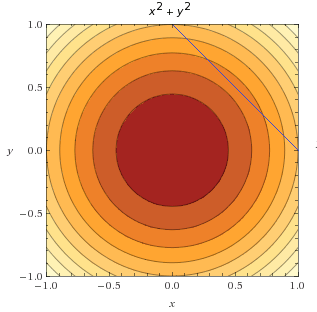
یافت لاگرانژ چه بود؟ او فهمید که مینیمم تابع ![]() تحت قید
تحت قید ![]() زمانی به دست میآید که گرادیانهای آنها به یک جهت اشاره کنند. اجازه دهدید ببینیم که ما چطور میتوانیم به یک نتیجه مشابه دست پیدا کنیم.
زمانی به دست میآید که گرادیانهای آنها به یک جهت اشاره کنند. اجازه دهدید ببینیم که ما چطور میتوانیم به یک نتیجه مشابه دست پیدا کنیم.
در شکل زیر میتوانیم نقطهای را در جایی که تابع هدف و مجموعه پاسخ مماس هستند مشاهده کنیم. ما همچنین تعدادی بردار گرادیان تابع به رنگ مشکی و تعدادی بردار گرادیان قید به رنگ سفید اضافه کردیم.
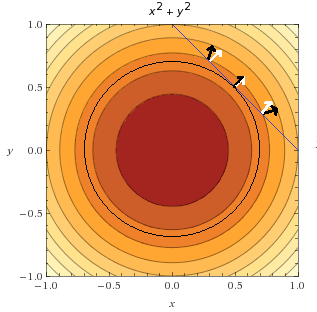
میتوانیم مشاهده کنیم که فقط یک نقطه است که در آن، دو بردار به یک جهت اشاره میکنند. (این همان مینیمم تابع هددف تحت قید است)
انگشت خود را روی نقطه اول در بالای شکل قرار دهید. اینجا شما در حال ارزیابی تابع هدف هستید و متوجه خواهید شد که یک مقدار ![]() را بر میگرداند. حال میخواهید بدانید که آیا مقدار کوچکتری هم وجود دارد یا نه. شما باید روی خط آبی بمانید و در غیر این صورت قید نسأله نقض خواهد شد. پس شما فقط میتوانید روی این خط به سمت راست و چپ حرکت کنید.
را بر میگرداند. حال میخواهید بدانید که آیا مقدار کوچکتری هم وجود دارد یا نه. شما باید روی خط آبی بمانید و در غیر این صورت قید نسأله نقض خواهد شد. پس شما فقط میتوانید روی این خط به سمت راست و چپ حرکت کنید.
اگر شما به سمت چپ حرکت کنید مشاهده میکنید که گرادیان تابع هدف به سمت چپ اشاره میکند. (به خاطر داشته باشید که این بردار همیشه به سمت مقدارهای بیشتر اشاره میکند) پس این ایده خوبی نیست. برای اطمینان میتوانید خودتان امتحان کنید و به سمت چپ حرکت کنید. مشاهده می کنید که تابع هدف ![]() را بر میگرداند. پس افزایش مییابد که قابل قبول نیست. اینبار به سمت راست حرکت کنید. تابع هدف
را بر میگرداند. پس افزایش مییابد که قابل قبول نیست. اینبار به سمت راست حرکت کنید. تابع هدف ![]() را بر میگرداند. این خوب است، شما دارید در جهت درست حرکت میکنید، پس ادامه دهید تا به نقطه مرکزی جایی که هر دو پیکان همجهت هستند برسید. اما همین که کمی حرکت کنید، متوجه میشوید که تابع هدف دوباره افزایش مییابد و همین که شما دیگر با با حرکت کردن به سمت چپ یا راست باعث افزایش تابع نشوید، میتوانید نتیجه بگیرید که این نقطه مینیمم است.
را بر میگرداند. این خوب است، شما دارید در جهت درست حرکت میکنید، پس ادامه دهید تا به نقطه مرکزی جایی که هر دو پیکان همجهت هستند برسید. اما همین که کمی حرکت کنید، متوجه میشوید که تابع هدف دوباره افزایش مییابد و همین که شما دیگر با با حرکت کردن به سمت چپ یا راست باعث افزایش تابع نشوید، میتوانید نتیجه بگیرید که این نقطه مینیمم است.
این چطور به زبان ریاضی ترجمه میشود؟
لاگرانژ به ما گفت که برای یافتن مینیمم یک تابع قیددار، ما باید به نقطههایی توجه کنیم که در آنها:
![]()
اما ![]() چیست و از کجا میآید؟
چیست و از کجا میآید؟
این همان چیزی است که ما به آن ضریب لاگرانژ میگوییم. به علاوه اگر دو بردار گرادیان به یک جهت اشاره کنند، ممکن است که طول یا اندازه یکسانی نداشته باشند، پس باید ضریب(های) ![]() وجود داشته باشد که اجازه دهد یکی به دیگری تبدیل شود.
وجود داشته باشد که اجازه دهد یکی به دیگری تبدیل شود.
توجه کنید که این فرمول نیاز ندارد تا گرادیانها در یک جهت باشند (ضرب کردن در یک عدد منفی جهت را تغییر خواهد داد)، فقط باید موازی باشند. به همین دلیل است که میتواند برای پیدا کردن هم ماکزیمم و هم مینیمم باهم استفاده شود (اگر می خواهید بدانید چطور، مثال ۱ این مقاله را ببینید).
چطور نقطههایی را پیدا کنیم که 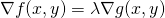 ؟
؟
توجه کنید که، ![]() برابر است با:
برابر است با:
![]()
برای سادهتر شدن، توجه داریم که اگر یک تابع را به صورت زیر تعریف کنیم:
![]() گرادیان برابر میشود با:
گرادیان برابر میشود با:
![]()
این تابع ![]() لاگرانژین نام دارد و حل کردن گرادیان لاگرانژین (حل کردن
لاگرانژین نام دارد و حل کردن گرادیان لاگرانژین (حل کردن ![]() ) یعنی پیدا کردن نقطههایی که در آنها گرادیانهای
) یعنی پیدا کردن نقطههایی که در آنها گرادیانهای ![]() و
و ![]() موازی باشند.
موازی باشند.
اجازه دهید این مثال را با استفاده از روش ضریبهای لاگرانژ حل کنیم!
به یاد داشته باشید، مسألهای که سعی داریم آن را حل کنیم، به صورت زیر است:
![]()
![]()
قدم اول: تابع لاگرانژین را معرفی میکنیم
![]()
و گرادیان آن به صورت زیر است:
![]()
قدم دوم: گرادیان آن را حل میکنیم
معادله زیر را حل میکنیم:
![]()
که یعنی باید دستگاه معادلات زیر را حل کنیم:
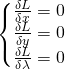
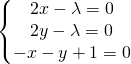
با ضرب کردن معادله دوم در -۱ و جمع کردن معادله اول و دوم داریم:
![]()
در نتیجه:
![]()
![]() را در معادله سوم جایگزین میکنیم:
را در معادله سوم جایگزین میکنیم:
![]()
![]()
![]()
![]()
در معادله اول ![]() را با
را با ![]() جایگزین میکنیم:
جایگزین میکنیم:
![]()
![]()
![]()
راه حلی پیدا کردیم که در آن ![]() ،
، ![]() و
و ![]() است.
است.
نتیجه میگیریم که مینیمم ![]() تحت قید
تحت قید ![]() به ازای
به ازای ![]() و
و ![]() به دست میآید.
به دست میآید.
اجازه دهید به کمک تحلیل گرافیکی، نشان دهیم که این راه حل روی نمودار شکل زیر نیز سازگار است:
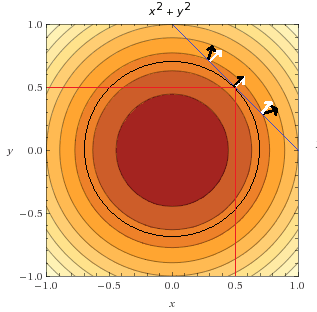
مینیمم تابع ![]() در
در ![]() و
و ![]() است
است
میتوانیم مشاهده کنیم که نقطه ![]() روی مجموعه پاسخ (خط آبی) قرار دارد و این همان نقطهای است که ما قبلا پیدا کرده بودیم.
روی مجموعه پاسخ (خط آبی) قرار دارد و این همان نقطهای است که ما قبلا پیدا کرده بودیم.
نتیجهگیری
در این پست، یک مفهوم مهم در بهینهسازی به نام دوگان را یاد گرفتیم. علاوه بر آن، کشف کردیم که یک مسأله بهینسازی میتواند قید تساوی و نامساوی نیز داشته باشد. در نهایت یاد گرفتیم که ضریبهای لاگرانژ چیست و چطور میتوانیم از آنها استفاده کنیم تا یک مسأله بهینهسازی با یک قید را حل کنیم.
اگر بخواهید درباره ضریبهای لاگرانژ در زمینه SVM بیشتر بدانید، میتوانید این مقاله خیلی خوب که نحوه استفاده آنها با قیدهای بیشتر را نشان می دهد مطالعه کنید.
قسمت بعدی چه زمانی آماده میشود؟
قسمت بعدی وجود ندارد، ولی در عوض درحال نوشتن کتابی درباره SVMها هستم که اگر قصد دارید درباره آنها بیشتر بدانید، مطالعه آن میتواند قدم بعدی شما باشد.
پانوشت(ها):
- ترجمه کردن بعضی از واژهها به فارسی واقعا مشکل هست. من تا جایی که تونستم سعی کردم که این کار رو انجام بدم. خیلی خوشحال میشم و استقبال میکنم اگر معادلهای فارسی مناسبی رو به من پیشنهاد بدید و معرفی کنید و البته پیشاپیش تشکر هم میکنم.
با سلام . کسایی که در مورد مباحث یادگیری ماشین مطالبی رو ارایه میدن زیادن و من سعی کردم یه نگاهی به بیشترشون بندازم . مطالبی رو که شما نوشتین علاوه بر زبان ساده و روان یه دید مفهومی رو برای خواننده شکل میده که کمتر مطلبی رو من به این زیبایی دیدم . واقعا جای تشکر داره و برای شما آرزوی موفقیت دارم .
سلام علی.
خیلی خوشحالم که همچین نظری رو نسبت به نوشتههام داری. امیدوارم در آینده بتونم ادامه بدم و کاملترش کنم.
موفق و سلامت باشی.
سلام.واقعا مردی خدایی دمت گرم.من کل آموزشتون مربوط به svm رو دقیق خوندم خیلی چیزها یاد گرفتم.واقعا مدیونتون هستم.خواهش می کنم ازتون کارهای اینچنینی در بقیه مباحث ریاضیات و علوم کامپیوتر باز هم انجام بدید. من رشتم هوش مصنوعی هست و مطالبتون واقعا برام مفید هست.بازم ممنون
سلام سجاد عزیز.
خواهش میکنم، لطف داری. خیلی خوشحالم که چیزی که نوشتم براتون مفید بوده و استفاده کردین.اگر زمان بهم اجازه بده قصد دارم ادامه آموزشهای مربوط به SVM رو بنویسم. هر موقع نوشتمشون حتما با ایمیل بهت اطلاع میدم.
ممنون بابت نظرت.
بسیار عالی و مفید بود این مجموعه پست های شما! واقعا ممنون
سلام. خوشحالم که براتون مفید بوده. امیدوارم بتونم ادامه مجموعه رو امسال بنویسم.
سلام من دانشجوی دکتری هستم مقالات وپنیک مرور کردم سر درنیاوردم تا اینکه مطلاب ارزتده ای که شما لطف کردین مطالعه کردم البته با دقت ما رو بند خودتون کردین استاد
سلام علی جان.
نظر مثبت شما باعث خوشحالی و افتخار من هست و قطعا انگیزهای هست برای نوشتن ادامه این مجموعه.
امیدوارم که موفق باشید.
مرحبا به این فن بیان واقعا دست مریزاد استاد عزیز
سلام. ممنونم لطف دارید.