این قسمت پنجم از آموزش مفاهیم ریاضی پشت ماشین‌های بردار پشتیبان است. در این پست درباره تابع‌های محدب یاد می‌گیریم.
اگر قسمت‌های قبلی را هنوز مطالعه نکرده‌اید، می‌توانید آموزش را از قسمت اول با مطالعه مقاله:SVM – درک مفاهیم ریاضی مورد نیاز – قسمت اول شروع کنید.
مینیمم سراسری را چطور می‌توانیم پیدا کنیم؟
یک راه ساده برای پیدا کردن مینیمم سراسری وجود دارد:
- همه مینیمم‌های محلی را پیدا کنیم
- کم‌ترین آن‌ها را انتخاب کنیم. این همان مینیمم سراسری است.
رویکرد دیگر مطالعه درباره تابعی است که قصد داریم آن را کمینه کنیم. اگر این تابع محدب باشد، در این صورت می‌توانیم مطمئن باشیم که مینیمم محلی یک مینیمم سراسری است.
قضیه: یک مینیمم محلی برای یک تابه محدب، یک حداقل سراسری است. (اثبات در ادامه)
تابع‌های محدب
تابع محدب چیست؟
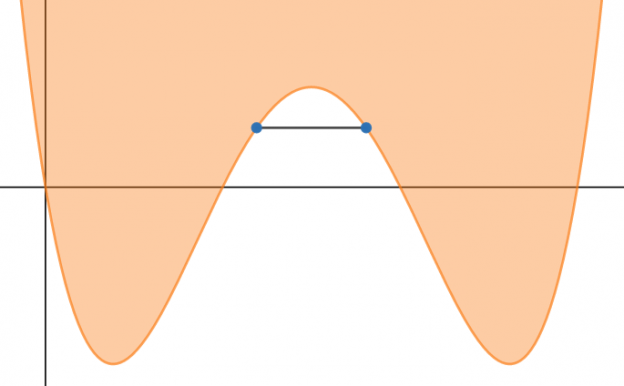
یک تابع محدب است، اگر بتوانید خطی بین دو نقطه از آن رسم کنید، بدون این که قسمت‌هایی از تابع، بین خط وصل کننده آن دو نقطه وجود نداشته باشد.
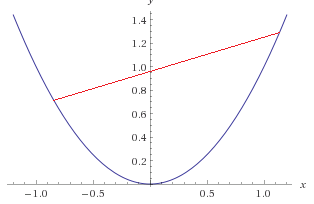
یک تابع محدب
و اگر که قسمتی از تابع را قطع کند در این صورت، تابع محدب نیست.
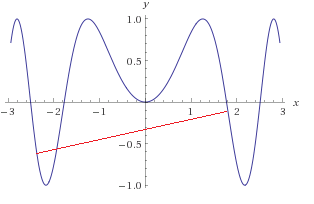
یک تابع غیر محدب
همان‌طور که در شکل بالا می‌بینید، خط قرمز تابع را قطع می‌کند و این یعنی تابع محدب نیست. توجه کنید که با این حال ممکن است که تابع در بعضی از بازه‌ها محدب باشد. برای مثال روی ![[-1, +1]](https://www.outlier.ir/wp-content/ql-cache/quicklatex.com-619c916c71821be3305793dd83311d5c_l3.png "Rendered by QuickLaTeX.com")
.
درباره تعریف دقیق‌تر تابع محدب می‌توانید این‌جا را مطالعه کنید.
ولی از الآن چیزی که مهم است بدانیم این است که پیدا کردن مینیمم سراسری یک تابع محدب آسان است.
مثل همیشه، یک مفهوم “عکس” هم وجود دارد. تابع 
مقعر است اگر 
محدب باشد.
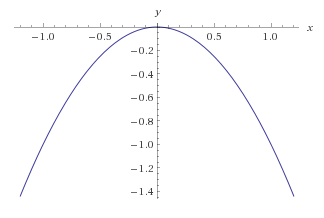
یک تابع مقعر
مشکل در این‌جا این است که تعریف اصلی ما “می‌توان خطی بین دو نقطه از تابع بدون این‌که خط دیگری را قطع کند، رسم کرد…” از یک تابع محدب نیز صحیح است.
ولی ریاضی‌دان‌ها تعریف دقیق‌تری دارند، آن‌ها می‌گویند:
یک تابع محدب است، زمانی که epigraph (مجموعه‌ای از نقطه‌های روی ) آن، یک مجموعه محدب باشد.
اما مجموعه محدب چیست؟
در فضای اقلیدسی، یک مجموعه محدب نلحیه‌ای است که برای هر جفت از نقطه‌های دلخواه درون یک محدوده، اگر خط راستی رسم کنیم که آن دو نقطه را به هم وصل کند، هر نقطه دلخواه روی آن خط نیز همچنان روی آن محدوده باشد. (ویکی‌پدیا)
مانندقبل ما نیز از منطق یکسانی استفاده می‌کنیم. یک مجموعه از نقطه‌ها محدب است اگر ما دو نقطه که متعلق به آم مجموعه هستند را انتخاب کنیم و خطی بین آن‌ها رسم کنیم، آن خط درون مجموعه باشد.
کدام مجموعه محدب و کدامیک غیر محدب است؟
اگر درست حدس زده باشید، مجموعه‌های دایره و مثلث محدب هستند. در شکل زیر، من یک خط قرمز بین دو نقطه رسم کردم. همان‌طور که می‌بینید، خط وصل کننده نقطه‌ها در ستاره، نشان می‌دهد که آن یک مجموعه محدب نیست.
ستاره یک مجموعه محدب نیست
می‌توانیم از این روش برای تشخیص محدب بودن تابع استفاده کنیم.
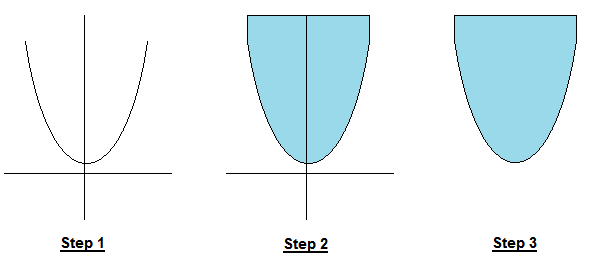
- قدم اول: تابعی داریم که می‌خواهیم محدب بودن آن را تشخیص دهیم
- قدم دوم: epigraph آن را در نظر می‌گیریم (فرض کنید آن را با آب پر می‌کنیم به‌طوری که با اضافه شدن آب، سرریز اتفاق نیفتد)
- قدم سوم: اگر شکل epigraph تابع محدب بود، در این صورت این تابع محدب است!
چطور بدانیم که یک تابع محدب است؟
فهمیدن تعریف epigraph ساده است، ولی مصورسازی تابع‌هایی با چند متغیر، مشکل است. پس ما باید درباره تابع مطالعه کنیم.
به طور کلی، یک تابع چند متغیره پیوسته که مشتق آن نیز موجود باشد روی یک مجموعه محدب، محدب است اگر و فقط اگر ماتریس Hessian آن روی داخل مجموعه محدب، semidefinite مثبت باشد. (ویکی‌پدیا)
اگر بخواهیم که محدب بودن تابع را بررسی کنیم، یک راه حل ساده، استفاده از دوست قدیمی‌مان ماتریس Hessian است. اگرچه به جای بررسی کردن این که همیشه مثبت است، مانند کاری که در پست قبلی کردیم، این بار باید بررسی کنیم که semidefinite مثبت باشد.
تفاوت آن‌ها در چیست؟
قضیه:
عبارت‌های زیر با هم برابرند:
- ماتریس متقارن
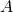مثبت semidefinite است. - همه eigenvalueهای 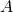غیر منفی هستند.
- همه principal minorهای 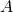غیر منفی هستند.
- ماتریس nonsingular مربعی
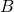به قسمی که 
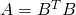وجود دارد. (منبع)
مانند قبل ما از minorها استفاده خواهیم کرد. با این تفاوت که ما باید همه principal minorها را بررسی کنیم، نه فقط leading principal minorها. به علاوه آن‌ها باید غیر منفی باشند. (یک عدد مثبت است، اگر بزرگ‌تر از صفر باشد. یک عدد غیر منفی است اگر بزرگ‌تر یا مساوی صفر باشد).
مثال: آیا تابع موزی محدب است؟
دیدیم که Hessian تابع موزی ما برابر بود با:
![\[\nabla ^2 f(x,y) = \begin{pmatrix} 1200x^2 - 400y +2 & -400x \\ -400x & 200 \end{pmatrix}\]](https://www.outlier.ir/wp-content/ql-cache/quicklatex.com-937dce8d388ddad14a3fc6605f72625b_l3.png "Rendered by QuickLaTeX.com")
principal minorهای مرتبه ۱ آن برابر هستند با:
برابر ۲۰۰ است (سطر ۱ و ستون ۱ را حذف کردیم).
برابر 
است (سطر ۲ و ستون ۲ را حذف کردیم).
اگر تابع محدب باشد، این minorها باید روی داخل مجموعه محدب غیر منفی باشند. کدام مجموعه محدب؟ طبق تعریف، دامنه یک تابع محدب، مجموعه محدب است. در مورد مسأله ما، وقتی می‌گوییم که یک تابع روی مجموعه محدب، محدب است، درباره دامنه آن صحبت می‌کنیم.
محدودیت “روی داخل” به ما می‌گوید که نباید نقطه‌هایی را انتخاب کنیم که روی مجموعه مرزی هستند.
در مورد مثال ما، تابع روی 
تعریف شده است که فضایی محدب است. پس ما می‌خواهیم اثبات کنیم که برای هر نقطه‌ای که انتخاب می‌کنیم، principal minorها غیر منفی هستند.
مشاهده می‌کنیم که minor همیشه مثبت است. ولی به راحتی می‌توانیم نقطه‌ای پیدا کنیم که باعث می‌شود غیر منفی باشد. به عنوان مثال: برای نقطه 
است.
در نتیجه، ما می‌توانیم بگوییم که تابع موزی محدب نیست.
این به ما می‌گوید که چندین راه برای اثبات محدب بودن تابع وجود دارد. برای راهنمایی بیشتر درباره این موضوع، شما را به قسمت ۲.۱ این مقاله ارجاع می‌دهم.
چرا تابع‌های محدب برای ما جذاب هستند؟
اولا دیدیم که مینیمم محلی تابع محدب، یک مینیمم سراسری است. این نتیجه‌ای نسبتا خوب، برای پیدا کردن سریع‌تر یک راه حل به ما کمک می‌کند.
به علاوه، در کل حل کردن مسأله‌های بهینه‌سازی محدب آسان‌تر است. چرا؟
برای بهتر متوجه شدن، شکل زیر را در نظر بگیرید.
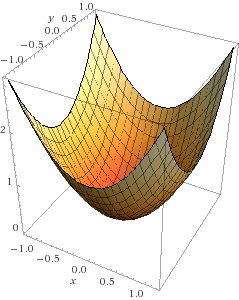
یک سطح محدب
تصور کنید که حل کردن یک مسأله بهینه‌سازی، مانند انداختن یک تیله روی یک سطح است. در مورد یک سطح محدب مانند چیزی که در شکل بالا مشاهده می‌کنید، اهمیتی ندارد که شما تیله را کجا می‌اندازید، تیله مستقیم به مرکز شکل خواهد رفت که در واقع همان مینیمم تابع است.
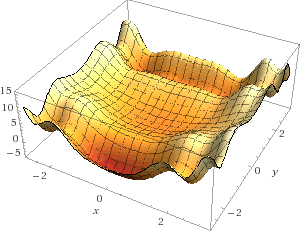
یک سطح غیر محدب
اگر سطح محدب نباشد چی؟ خب همان‌طور که می‌بینید، انداختن یک تیله روی سطح شانس زیادی برای رفتن به یک مینیمم محلی دارد. در چنین شرایطی چه باید کرد؟ تیله را برای رفتن به یک جای دیگر دوباره می‌اندازید؟ همان‌طور که می‌بینید، مسأله به این سادگی‌ها هم نیست.
مثال تیله از این نظر که اساسا همان کار یک الگوریتم بهینه‌سازی به نام کاهش گرادیان (Gradient descent) انجام می‌دهد، جالب است. یک راه دیگر برای حل یک مسأله بهینه‌سازی، استفاده از روش معروف نیوتن است. (خواننده‌های علاقمند را به مطالعه دقیق‌تر این روش ها و حتی پیاده‌سازی آن‌ها تشویق میکنم.)
نتیجه‌گیری
در این پست یاد گرفتیم که یک مجموعه محدب چیست و چگونه محدب بودن یک تابع را مشخص کنیم. به علاوه دیدیم که نمایش بصری به ما نشان می‌دهد که چرا بهینه‌سازی محدب معمولا ساده‌تر از بهینه‌سازی غیر محدب است: به این خاطر که آن‌ها مینیمم محلی ندارند.
محدب بودن یک مفهوم مهم است که به فهمیدن بهینه‌سازی کمک می‌کند. حال که بهتر آن را می‌شناسیم، با یک جنبه مهم دیگر به نام “دوگان” آشنا خواهیم شد. در نهایت خواهیم دید که چطور می‌توانیم مسأله‌های بهینه سازی مشکل‌تر را حل کنیم. قسمت ششم این سری آموزشی را برای فهمیدن این موضوع مطالعه فرمایید! ممنون که تا این‌جای کار با من بودید.
پانوشت(ها):
- ترجمه کردن بعضی از واژه‌ها به فارسی واقعا مشکل هست. من تا جایی که تونستم سعی کردم که این کار رو انجام بدم. خیلی خوشحال میشم و استقبال میکنم اگر معادل‌های فارسی مناسبی رو به من پیشنهاد بدید و معرفی کنید و البته پیشاپیش تشکر هم میکنم.
سلام چرا توی برازش منحنی به روش خطا مربعات تابع محدب است?
سلام ریحانه.
مرسوم هست که مقدار فاصله (خطا) به توان ۲ برسد تا از مثبت بودن این مقدار اطمینان حاصل شود. همچنین این کار باعث مشتق‌پذیر شدن تابع خطا خواهد شد.
و اما علت محدب بودنش هم این هست که ما یک سری مقدار (خطاها) رو به توان ۲ رسوندیم، پس مقدار منفی نداریم، فقط این مقدار‌ها کم و زیاد می‌شوند. و شکل نمودار درجه ۲ هم که از قبل برای ما آشنا هست. (U)
سعی کردم که ساده توضیح بدم و امیدوارم که منظورم رو متوجه شده باشید.
سلام ببخشید چرا نیم فضا و فوق صفحه محدب است میشه بگین
سلام. داخل همین پست توضیح داده شده. قسمت: چرا تابع‌های محدب برای ما جذاب هستند؟
امیدوارم جوابتون رو اونجا پیدا کنید.
سلام آموزش بسیار کامل و جامعی بود ؟ایا کتاب یا نوشته ی دیگه ای درباره این موضوع نوشتین؟اگر نوشتین ممنون میشم معرفی کنید که بتونیم استفاده کنیم .
سلام. ممنون بابت نظرتون.
ادامه این آموزش رو دارم آماده میکنم ولی چون زمان محدودی دارم یکم کند پیش میره کار.